Paper Reading: Efficient Estimation of Word Representations in Vector Space
Mikolov, T., Chen, K., Corrado, G., & Dean, J. (2013). Efficient estimation of word representations in vector space. arXiv preprint arXiv:1301.3781.
Related Work
| Method | Strength | Drawback |
|---|---|---|
| Treat words as atomic units | simplicity, robustness, and the observation that simple models trained on huge amounts of data outperform complex systems trained on less data | no notion of similarity between words |
Neural network based language models significantly outperform N-gram models.
Goals
- Introduce techniques that can be used for learning high-quality word vectors from huge data sets with billions of words
- Word vectors between 50-100
- Multiple degrees of similarity
- e.g. vector(‘King’) - vector(‘Man) + vector(‘Woman’) ≈ vector(‘Queen’)
- maximize accuracy of these vector operations by developing new model architectures
Definition
- Computational complexity of a model = the number of parameters that need to be accessed to fully train the model
- The training complexity is proportional to $O = E\times T\times Q$
- $E$: the number of the training epochs
- $T$ : the number of the words in the training set
- $Q$: defined further for each model architecture
Model Architectures
Feedforward Neural Net Language Model (NNLM)
NNLM has been proposed in the paper A Neural Probabilistic Language Model.
- Input layer
- $N$ previous words are encoded using 1-of-V coding, where $V$ is size of the vocabulary
- Projection layer $P$
- has dimensionality $N\times D$, using a shared projection matrix
- Hidden layer $H$
- is used to compute probability distribution over all the words in the vocabulary
- Output layer
- dimensionality $V$
The computational complexity per each training example is
\[Q = N\times + N\times D\times H +H\times V\]Use hierarchical softmax where the vocabulary is represented as a Huffman binary tree.
Recurrent Neural Net Language Model (RNNLM)
- Specify the context length
- Use RNN model to represent more complex pattern than than the shallow
- Structure
- Input layer
- Hidden layer
- Output layer
The complexity per training example of the RNN model is
\[Q = H\times H+H\times V\]Parallel Training of Neural Networks
New Log-linear Models
replace(neural network, simple model)
- faster: possibly be trained on much more data efficiently
- less accurate
- Continuous word vectors are learned using simple model
- The N-gram NNLM is trained on top of these distributed representations of words.
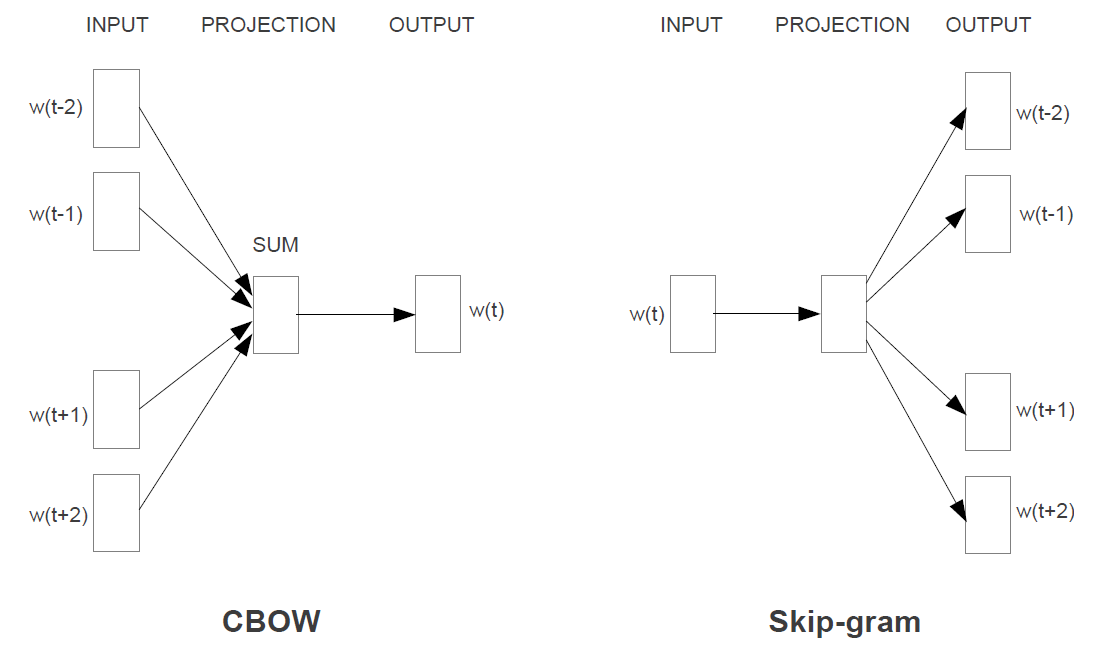
CBOW: Continuous Bag-of-Words Model
- The non-linear hidden layer: removed
- The projection layer: shared for all words
The order of words in the history does not influence the projection
Building a log-linear classifier with four feature and four history words at the input
Training complexity
\[Q = N\times D + D\times \log_2(V)\]Continuous Skip-gram Model
Goal: maximize classification of a word based on another word in the same sentence
Predict words within a certain range before and after the current word.
Training complexity of this architecture is proportional to
\[Q = C\times (D+D\times \log_2(V))\]- $C$ is the maximum distance of the words
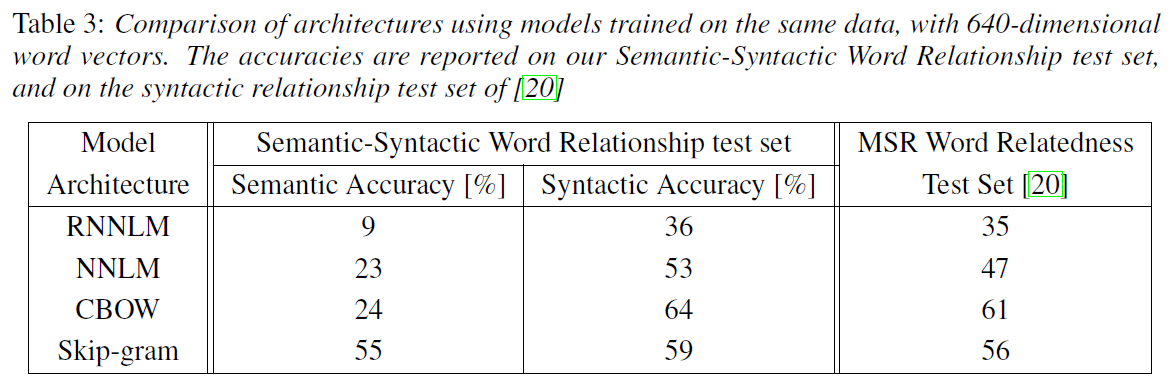
Experiments
When training high dimensional word vectors on a large amount of data, the resulting vectors can be used to answer very subtle semantic relationship between words.
Task Description
Question
- five types of semantic questions
- nine types of syntactic questions
Evaluation
Evaluate the overall accuracy for all question types
- Question is assumed to be correctly answered only if the closet word to the vector computed using the above methods is exactly the same as the correct word in the question.
Data
- Google News corpus
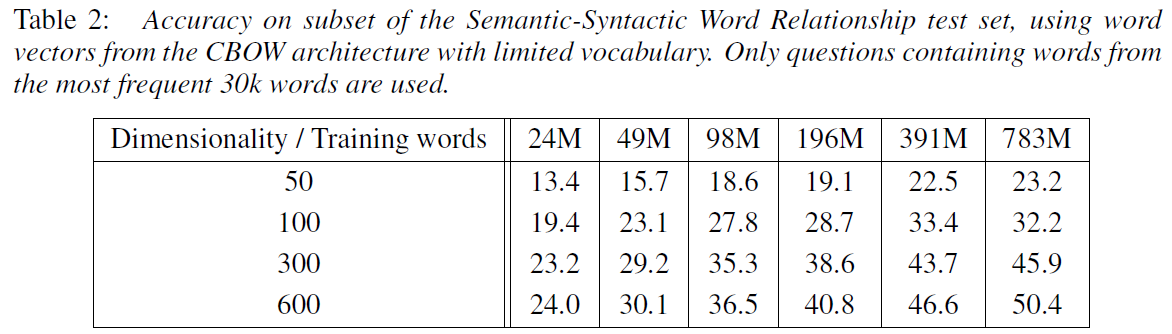
Maximization of Accuracy
We have to increase both vector dimensionality and the amount of the training data together.