Lecture 1: Introduction and Word Vectors

The result that word meaning can be represented rather well by large vector of real numbers.

1. The course

fundamental knowledge
Advanced Technology
practise: PyTorch

2. Human language and word meaning

How to get computers to understand language.

How do we present the meaning of a word?

symbmol $\Leftrightarrow$ idea or thing
denotational semantics

Traditional NLP solution:

WordNet, a thesaurus containing lists of synonym sets and hypernyms
- great as a resource but missing nuance
  - only correct in some contexts
- missing new meanings of words
  - impossible to keep up-to-date
- subjective
- requires human labor to create and adapt
- can’t compute accurate words similarity
one-hot vectors
- regard words as discrete symbols
- HUGE vector dimensions
- no natural similarity for one-hot vectors

Solution

learn to encode similarity in the vectors themselves
Distributional semantics: a word’s meaning is given by the words that frequently appear close-by
When a word $w$ appears in a text, its context is the set of words that appear nearby(within a fixed-size window)
Use the many contexts of $w$ to build up a representation of $w$

Word vectors

We will build a dense vector for each word, chosen so that it is similar to vectors of words that appear in similar contexts.
Word vectors are also called word embeddings or (neural) word representations. They are a distributed representation.

3. Word2vec introduction

Word2vec (Mikolov et al. 2013) is a framework for learning word vectors.

Idea:

We have a learge corpus (“body”) of text
Every word in a fixed covabularty is represented by a vector
Go through each position $t$ in the text, which has a center word $c$ and context (“outside”) words $o$
Use the similarity of word vectors for $c$ and $o$ to calculate the probability of $o$ given $c$ (or vice versa)
Keep adjusting the word vectors to maximize this probability.

4. Word2vec objective function

Goal

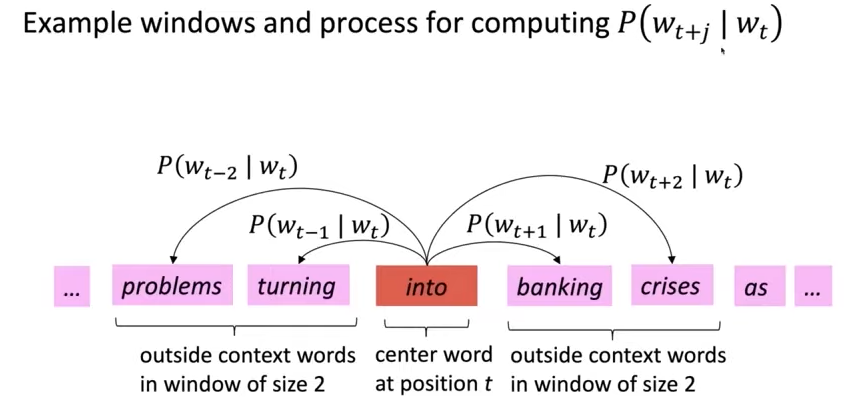
For each position $t = 1,…,T$, predict context words within a window of fixed size $m$, given center word $w_j$. Data likelihood:

\[\textrm{Likelihood} = L(\theta) = \prod_{t=1}^T\prod_{-m\le j\le m \& j\not ={0}} P(w_{t+j}|w_t;\theta)\]

$\theta$ is all variables to be optimized $\prod_{t=1}^T$: using each wor as a center word

Objective function

The objective function(cost function, loss function) $J(\theta)$ is the (average) negative log likelihood

\[J(\theta) = -\frac{1}{T} \log L(\theta) = -\frac{1}{T}\sum_{t=1}^T\sum_{-m\le j\le m \& j\not ={0}} \log P(w_{t+j}|w_t;\theta)\]

Minimizing objective function $\Leftrightarrow$ Maximizing predictive accuracy

$v_w$ when $w$ is a center word
$u_w$ when $w$ is a context word
Then for a center word $c$ and a context word $o$ (softmax) $P(o|c) = \frac{\exp(u_o^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}$

softmax function maps arbitrary values $x_i$ to a probability distribution $p_i$

$\mathbb{R}^n \rightarrow [0, 1]^n$

“max” because amplifies probability of largest $x_i$(but returns a distribution)

“soft” because still assigns some probability to smaller $x_i$ Frequently used in Deep learning

Gradient

\[\begin{align} \frac{\partial}{\partial v_c} \log P(o|c) &= \frac{\partial}{\partial v_c} \log \frac{\exp(u_o^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)}\\ &= \frac{\partial}{\partial v_c} \log \exp(u_o^Tv_c)- \frac{\partial}{\partial v_c} \log \sum_{w\in V}\exp(u_w^Tv_c) \\ &= \frac{\partial}{\partial v_c} u_o^Tv_c - \frac{\partial}{\partial v_c} \log \sum_{w\in V}\exp(u_w^Tv_c) \\ &= u_o - \frac{\partial}{\partial v_c} \log \sum_{w\in V}\exp(u_w^Tv_c) \\ &= u_o - \frac{1}{\sum_{w\in V}\exp(u_w^Tv_c)}\times \frac{\partial}{\partial v_c}\sum_{w\in V}\exp(u_w^Tv_c) \\ &= u_o - \frac{1}{\sum_{w\in V}\exp(u_w^Tv_c)}\times \sum_{w\in V}\frac{\partial}{\partial v_c}\exp(u_w^Tv_c) \\ &= u_o - \frac{1}{\sum_{w\in V}\exp(u_w^Tv_c)}\times \sum_{w\in V}\exp(u_w^Tv_c) \frac{\partial}{\partial v_c} u_w^Tv_c\\ &= u_o - \frac{1}{\sum_{w\in V}\exp(u_w^Tv_c)}\times \sum_{w\in V}\exp(u_w^Tv_c) u_w\\ &= u_o - \frac{\sum_{w\in V}\exp(u_w^Tv_c) u_w}{\sum_{w\in V}\exp(u_w^Tv_c)}\\ &= u_o - \sum_{x\in V}\frac{\exp(u_x^Tv_c)}{\sum_{w\in V}\exp(u_w^Tv_c)} u_x\\ &= u_0 - \sum_{x=1}^V p(x|c) u_x \\ &= \textrm{observed} - \textrm{expected} \end{align}\]