Computer Organization
$Ericaaaaaaaa$
$Jan,\ 2021$
组合逻辑设计
逻辑门电路
TTL、MOS 集成门电路
-
晶体管
-
COMS
-
N 型
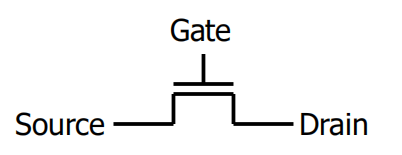
-
P 型
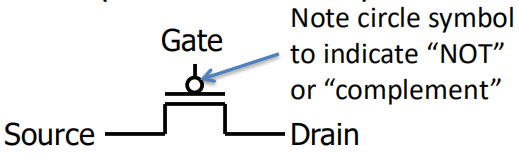
Gate N 型 P 型 0 (低电平) OFF (截止) ON (导通) 1 (高电平) ON (导通) OFF (截止) - 注意事项
- 导通时应该让
Sourse和Gate之间电压有反差 - 避免无源驱动
- 避免短路
- 导通时应该让
-
-
利用晶体管构建门电路
-
NAND
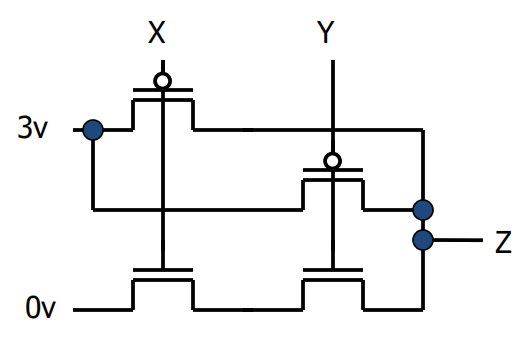
-
NOR
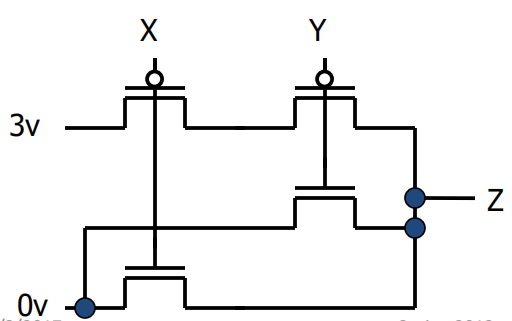
-
与门、非门、或门、复合逻辑门电路及其性能指标
-
门电路
名称 示意图 真值表 NOT 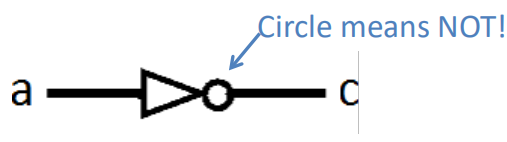
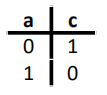
AND 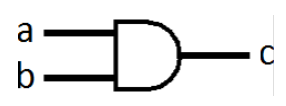
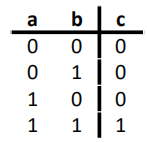
OR 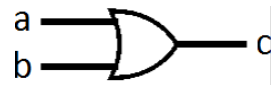
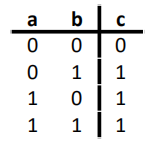
XOR 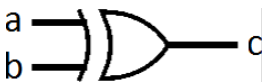
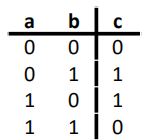
NAND 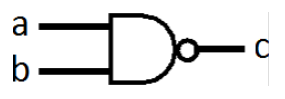
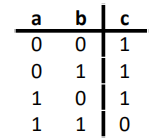
NOR 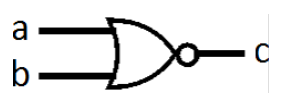
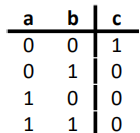
布尔代数
布尔代数基本原理
逻辑函数表达式:标准表达式(最小项表达式、最大项表达式)
逻辑函数表达式的简化法:(合并乘积项法、吸收项法、配项法)
-
合并乘积项法——利用互补律消去一个变量
$F = A(BC + \overline{B}\overline{C}) + AB\overline{C} + A\overline{B}C$
$\ \ \ \ =ABC + A\overline{B}\overline{C} + AB\overline{C} + A\overline{B}C$ 利用分配律展开
$\ \ \ \ =(ABC + A\overline{B}C) + (A\overline{B}\overline{C} + AB\overline{C}))$ 合并
$\ \ \ \ =AC(B + \overline{B}) + A\overline{C}(\overline{B} + B)$ 互补律
$\ \ \ \ =AC + A\overline{C}$ 互补律
$\ \ \ \ =A(C + \overline{C})$ 互补律
$\ \ \ \ =A$
-
吸收项法——利用吸收律和包含律减少“与”项
$F = A\overline{B} + \overline{A}B + ABCD + \overline{A}\overline{B}CD$
$\ \ \ \ =(A\overline{B} + \overline{A}B) + (AB + \overline{A}\overline{B})CD$
$\ \ \ \ =(A\overline{B}+\overline{A}B) + \overline{A\overline{B} + \overline{A}B}CD\ \ \ \ \ \ 吸收律: A \pm AB = A\pm B$
$\ \ \ \ =A\overline{B} + \overline{A}B + CD$
-
配项法——利用互补律,配在乘积项上
$F = AB + \overline{A}\overline{B}C + BC$
$\ \ \ \ =AB + \overline{A}\overline{B}C + BC(A +\overline{A})$
$\ \ \ \ =AB + \overline{A}\overline{B}C + ABC + \overline{A}BC$
$\ \ \ \ =(AB + ABC) + (\overline{A}\overline{B}C + \overline{A}BC)$
$\ \ \ \ =AB(1 + C) + \overline{A}C(B + \overline{B})$
$\ \ \ \ =AB + \overline{A}C$
-
卡诺图 $(K-map)$
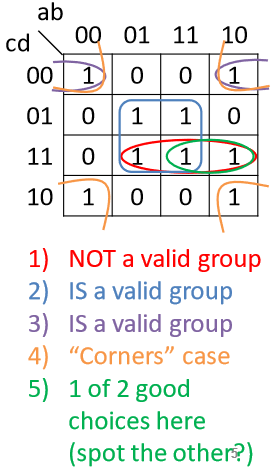
$y = bd + b’d’ + acd$
用卡诺图生成的最简表达式不唯一。
使用卡诺图可以方便的化简多个布尔表达式。
- 卡诺图采用格雷码,即相邻方格中有一个变量的值不同。
- 卡诺图是环绕的
- 用卡诺图得到最小化等式的规则
- 用最少的圈来圈住全部所有的1
- 每个圈中的所有方格都必须包含1
- 每个圈必须是矩形,其每个边长必须是 2 的整数次幂(例如 1, 2, 4)
- 每个圈必须尽可能的大
- 圈可以环绕卡诺图的边界
- 如果可以使用更少数量的圈,则卡诺图中一个为 1 的方格可以被多次圈住
Verilog HDL 介绍
【Verilog HDL】 是硬件描述语言的一种,用于数字电子系统设计。
【HDL】$Hardware\ Description\ Language$ 硬件描述语言
【VHDL】$VHSIC\ Hardware\ Description\ Language$ 高速集成电路硬件描述语言
【VHSIC】$Very\ High\ Speed\ Integrated\ Circuit$ 高速集成电路
基本组合逻辑部件设计与分析
运算单元电路(加法器、比较器)
-
一位全加器
-
末位
- 列出真值表
$a_0$ $b_0$ $s_0$ $c_1\ (Carry Out Bit)$ 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 - 通过真值表写出表达式
$s_0 = a_0\ XOR\ b_0$
$c_1 = a_0\ AND\ b_0$
-
其它位
- 列出真值表
$a_i$ $b_i$ $c_i$ $s_i$ $c_{i+1}\ (Carry Out Bit)$ 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1 -
通过真值表写出表达式
$s_i = \overline{a_i}\overline{b_i}c_i + \overline{a_i}b_i\overline{c_i} + a_i\overline{b_i}\overline{c_i} + a_ib_ic_i$
$c_{i+1} = a_ib_i + a_ic_i + b_ic_i$
-
根据表达式构造一位全加器
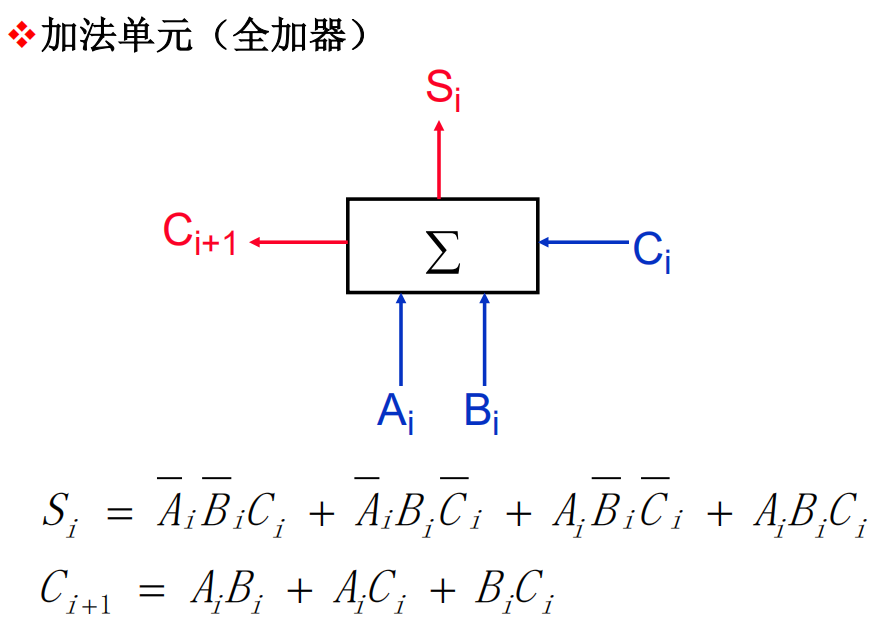
-
行波进位加法器
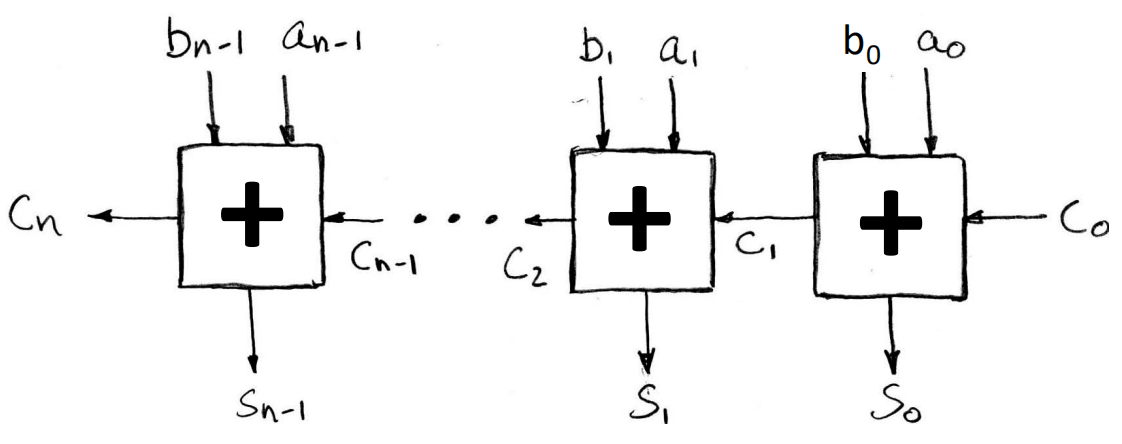
-
-
比较器
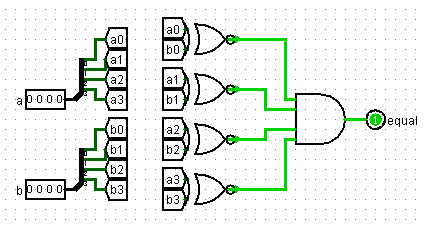
多路选择器,译码器,编码器
-
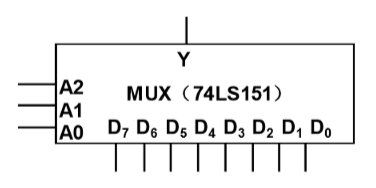
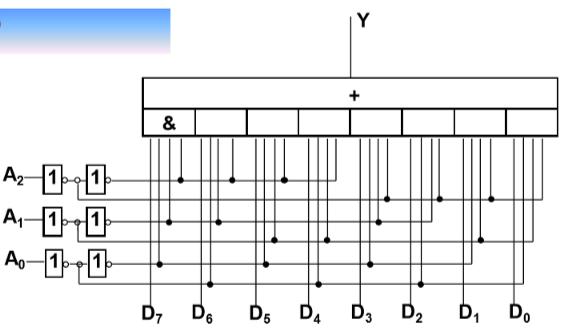
8 选 1 数据选择器
-
功能①
-
控制端共三位,为 $A_2A_1A_0$,通过 $A_0,\ A_1,\ A_2$ 的组合选择某个 $D$
-
$Y = \overline{A_2}\overline{A_1}\overline{A_0}D_0 + \overline{A_2}\overline{A_1}A_0D_1 + \overline{A_2}A_1\overline{A_0}D_2 + \overline{A_2}A_1A_0D_3 + A_2\overline{A_1}\overline{A_0}D_4 + A_2\overline{A_1}A_0D_5 + A_2A_1\overline{A_0}D_6 + A_2A_1A_0D_7$
$\ \ \ =m_0D_0 + m_1D_1 + m_2D_2 + m_3D_3 + m_4D_4 + m_5D_5 + m_6D_6 + m_7D_7$
-
-
功能②
-
$D_7 - D_0$ 为控制端——多功能运算电路
通过 $D_7 - D_0$ 取不同的值,从输入变量 $A_2,\ A_1,\ A_0$ 的各个最小项中选取某几个最小项输出,实现不同的运算电路。
共 $2^8 = 256$ 种功能——包含 3 变量的各种最小项表达式,可实现任意组合逻辑电路的设计
-
$Y = \overline{A_2}\overline{A_1}\overline{A_0}D_0 + \overline{A_2}\overline{A_1}A_0D_1 + \overline{A_2}A_1\overline{A_0}D_2 + \overline{A_2}A_1A_0D_3 + A_2\overline{A_1}\overline{A_0}D_4 + A_2\overline{A_1}A_0D_5 + A_2A_1\overline{A_0}D_6 + A_2A_1A_0D_7$
$\ \ \ =m_0D_0 + m_1D_1 + m_2D_2 + m_3D_3 + m_4D_4 + m_5D_5 + m_6D_6 + m_7D_7$
-
【例】利用数据选择器实现逻辑函数 $F(A, B, C) = \overline{A}\overline{B}C + \overline{A}B\overline{C} + AB$
【解】
$A-A_2, B-A_1, C-A_0$
$F(A, B, C) = \overline{A}\overline{B}C + \overline{A}B\overline{C} + AB = m_1 + m_2 + m_6 + m_7$
故:$A_0 = 0, D_1 = 1, D_2 = 1, D_3 = 0, D_4 = 1, D_5 = 0, D_6 = 1, D_7 = 1$
-
-
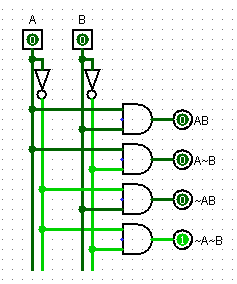
译码器
时序逻辑设计
锁存器和触发器
SR 锁存器,D 锁存器
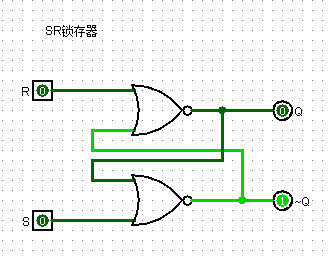
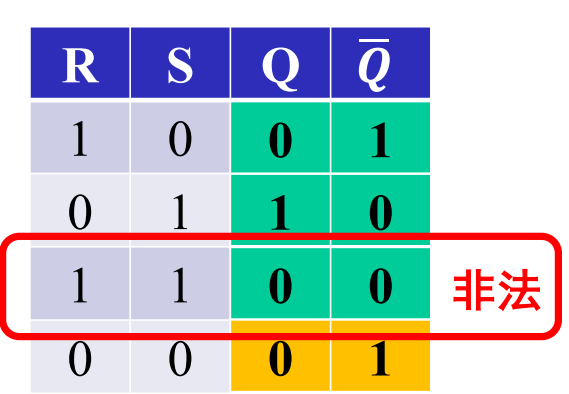
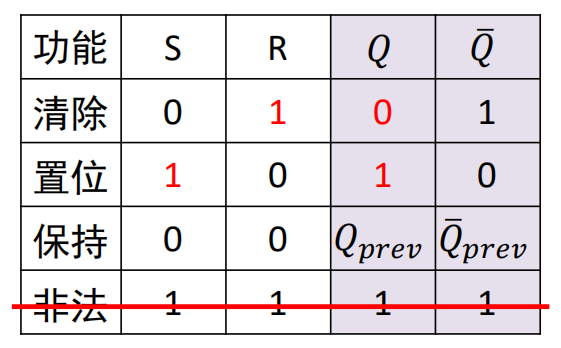
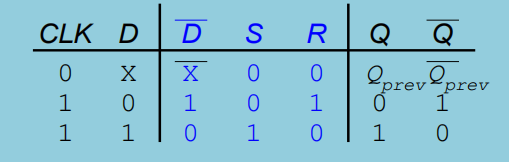
SR 锁存器
Q 与 ~Q 随着 R 与 S 的改变随时改变
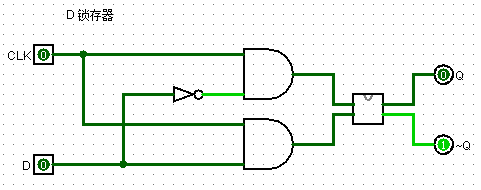
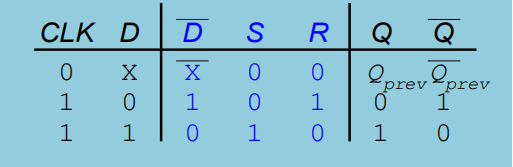
D 锁存器 (D-latch)
在 clk 置位时,D 实时改变 Q 与 ~Q,
在 clk 为0时,D 对 Q 与 ~Q 无影响
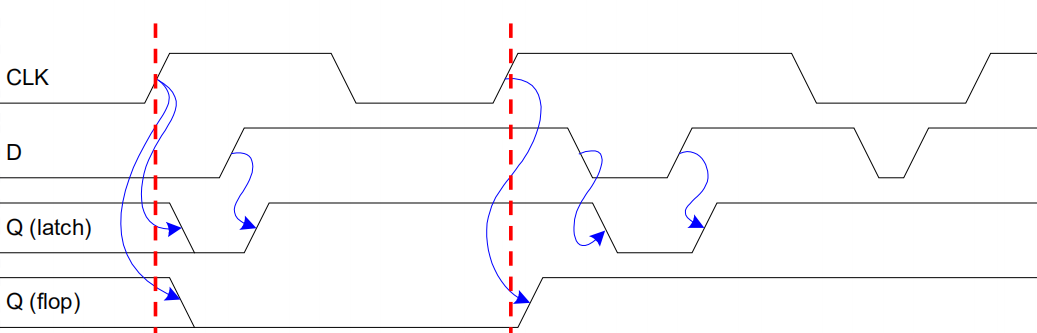
D 触发器 (D-flip flop)
在 clk 上升沿时,Q 同步更新为 D 的值
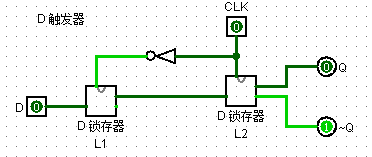
D Latch vs. D Flip-Flop
JK 触发器
有限状态机 Finite State Machine (FSM)
概述
- 状态:电路所处的特定工作阶段
- 状态寄存器:
- 状态寄存器的值:
- 次态逻辑:根据输入和当前状态的编码值,计算下一个状态编码值
- 次态逻辑也是组合逻辑
- 输出逻辑:根据状态及输入,计算该状态下的输出值
表示方法
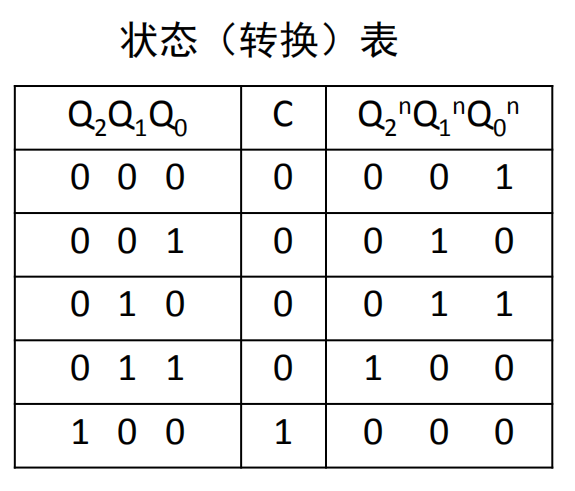
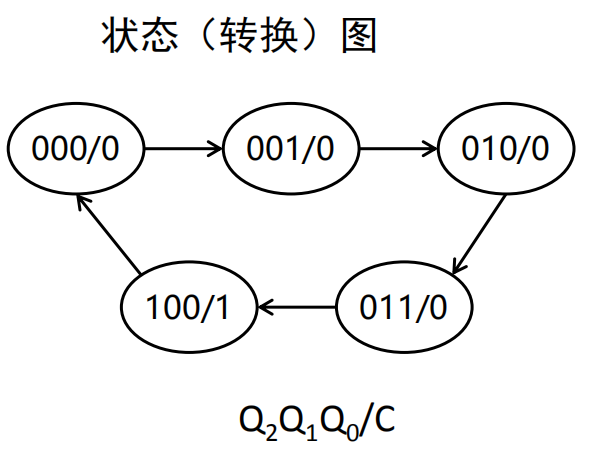
构造方法
-
规划状态总数
-
构造状态图
每个状态的转移条件必须是完备的
-
根据【输入信号、当前状态编码、下一个状态编码】构造每个寄存器的 D 输入信号的门电路
方法:真值表→乘积项表达式→最简表达式→最简门电路
-
根据设计需求决定当前状态的输出
设计要点
-
初始状态
-
复位信号
-
状态编码方式
- 二进制编码
- $\log_2^N$ 个触发器表示 $N$ 个状态
- 节约逻辑资源,但可能产生毛刺
- 格雷编码
- $\log_2^N$ 个触发器表示 $N$ 个状态
- 节约逻辑资源,但可能产生毛刺
- 一位独热编码(One Hot Encoding)
- 资源消耗多,但无毛刺
- 降低次态逻辑和输出逻辑的复杂度,有利于提高时钟频率
- FPGA 具有丰富的寄存器资源,采用一位独热码编码可以有效提高电路的速度和可靠性
状态 二进制编码 格雷编码 一位独热编码 0 000 000 00000001 1 001 001 00000010 2 010 011 00000100 3 011 010 00001000 4 100 110 00010000 5 101 111 00100000 6 110 101 01000000 7 111 100 10000000 - 二进制编码
Moore 型 FSM
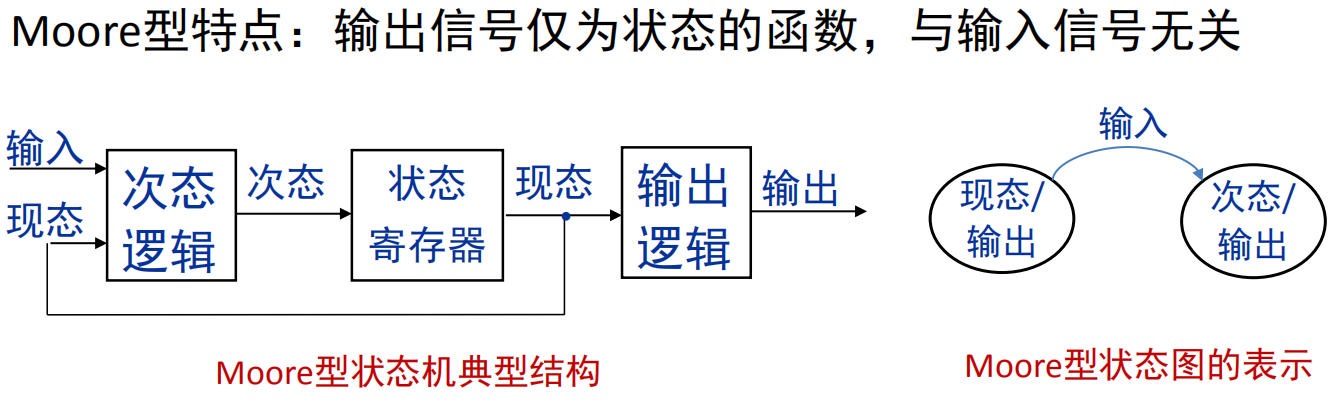
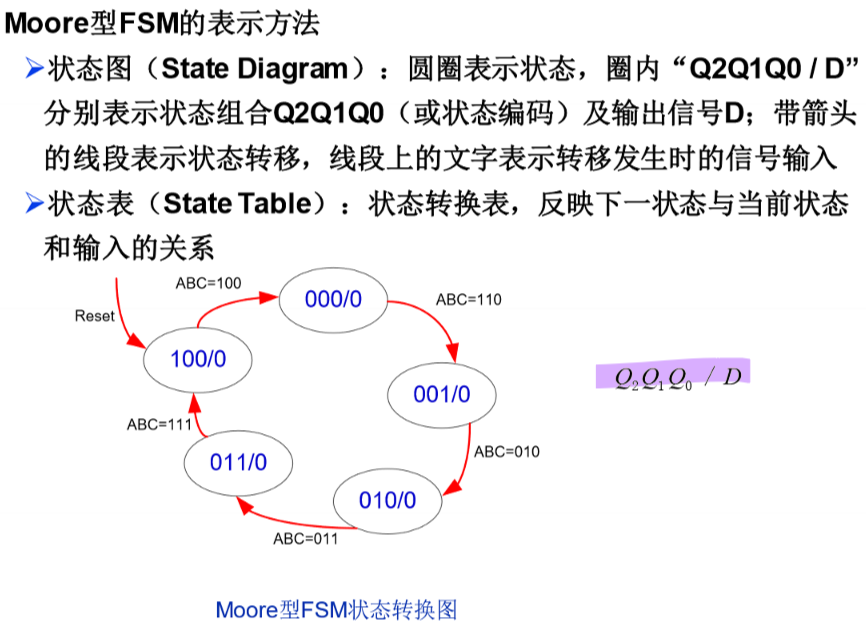
Mealy 型 FSM
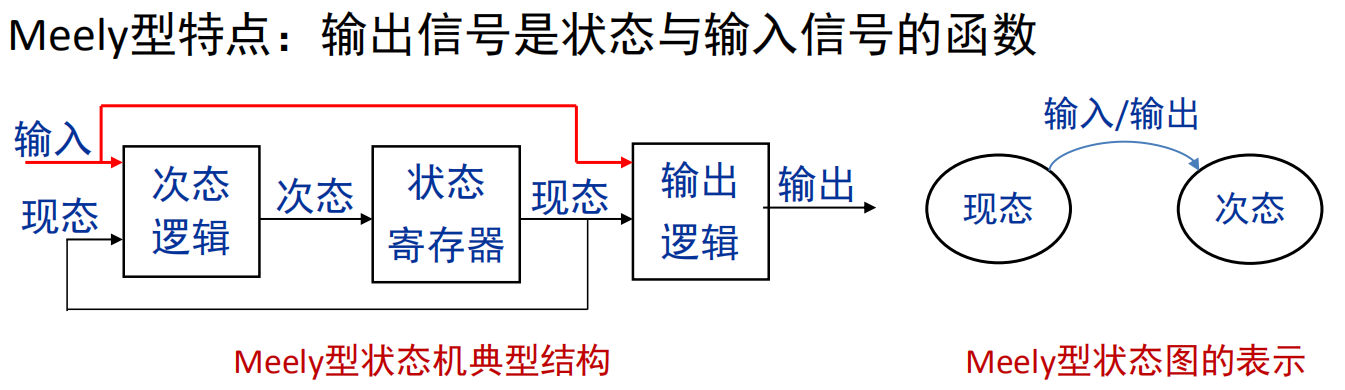
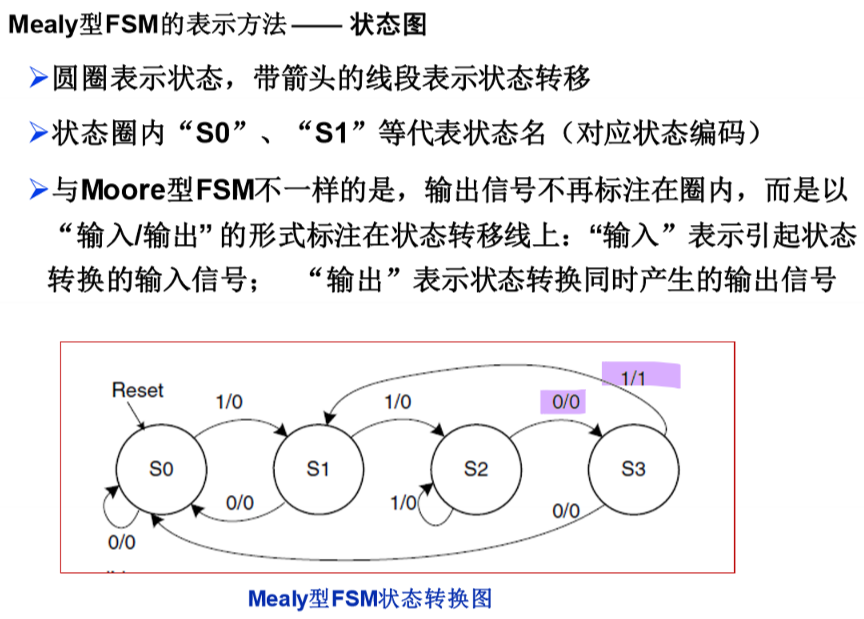
状态机类型的选择

时序逻辑电路分析
数据寄存器
移位寄存器
包括时钟、串行输入 $S_{in}$、串行输出$S_{out}$和 N 位并行输出 $Q_{N-1:0}$
移位寄存器可以看作是串行到并行的转换器。输入由 $S_{in}$以串行的方式提供(一次一位)。在 N 个周期后,前面的 N 位输入可以在 Q 中并行访问。
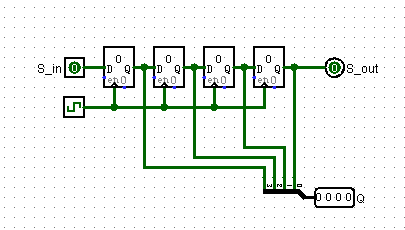
计数器
计数器 = 加法器 + 复位寄存器
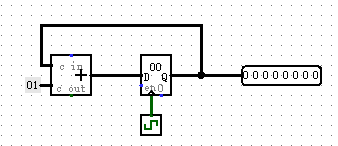
主存储器
存储单元电路
存储器阵列($memory\ array$)——可以有效存储大量数据
-
概述
-
位单元
存储器阵列由为单元
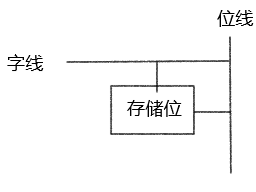 (bit cell)的阵列组成,其中每个为单元存储一位数据。
(bit cell)的阵列组成,其中每个为单元存储一位数据。 -
存储器的结构
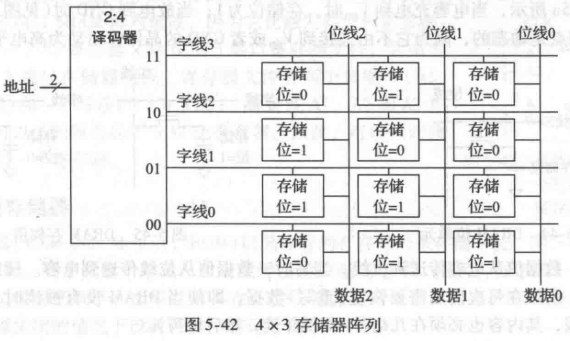
-
-
分类
- 动态随机访问存储器(DRAM)
- 静态随机访问存储器(SRAM)
- 只读存储器(ROM)
- 现代ROM不再只读,也可以写入。不同点在于ROM的写入时间更长,但是是非易失的。
RAM是易失型,关掉电源时会丢失数据;ROM是非易失型,没有电源也能无期限的保存数据。
SRAM 存储单元电路 Static Random Access Memory
不需要刷新存储位
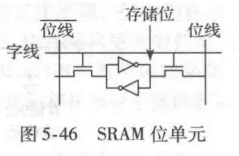
DRAM 存储单元电路 Dynamic Random Access Memory
以电容的充电和放电来存储位。位值存储在电容中,nMOS作为开关。字线作为MOS的开关
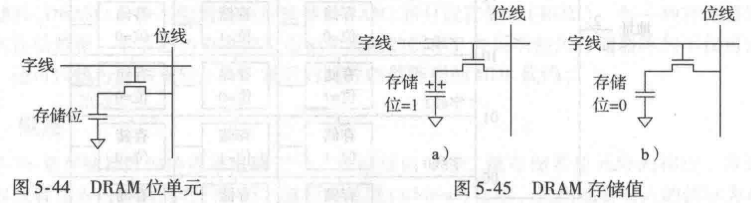
ROM 存储单元电路
以是否存在晶体管作为是否存储一位。在读过程中,位线被拉高,如果存在MOS,则位线被拉低,不存在MOS则保持高。

主存储器的结构
SRAM 芯片的内部结构
DRAM 芯片的内部结构
存储器的扩展
芯片容量的基本描述
字单元数 × 每个字单元的位数
-
1K × 2:1024个字单元,每个字单元 2 位(二进制位)

-
64 K × 8:

存储器的扩展方法

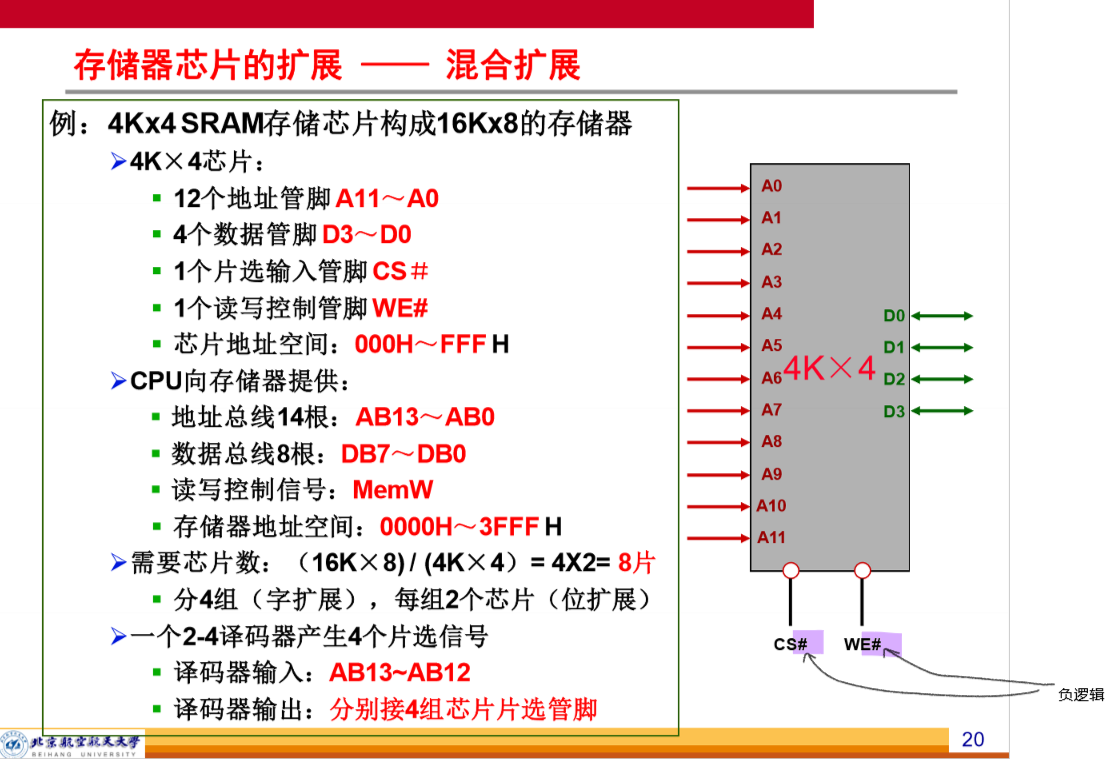
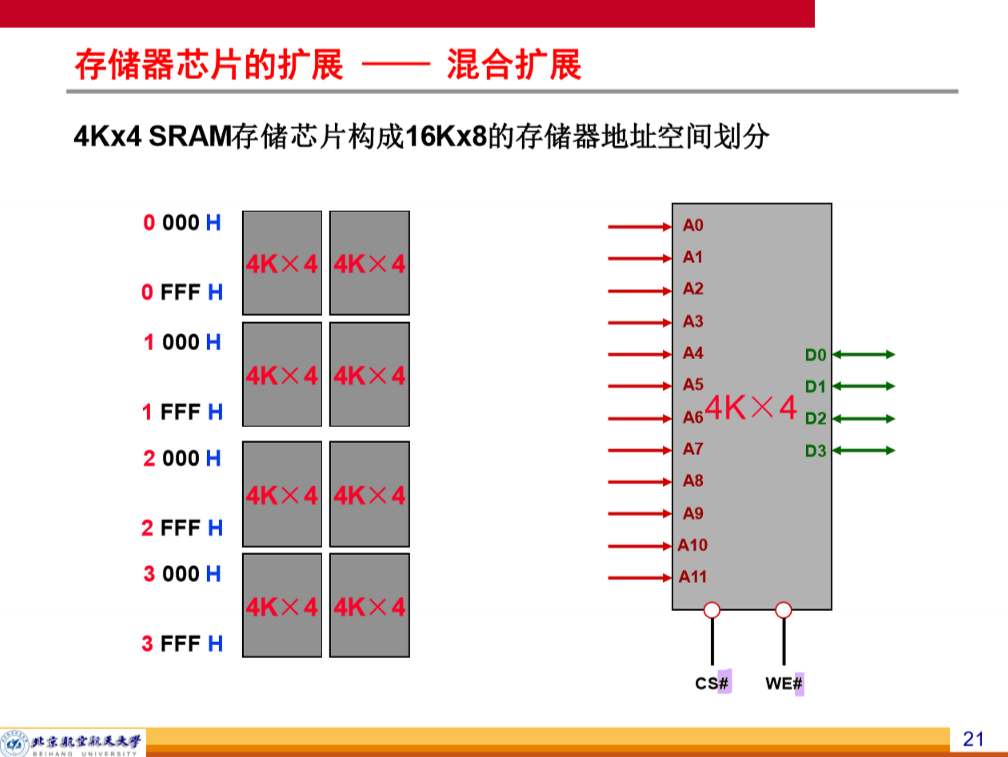
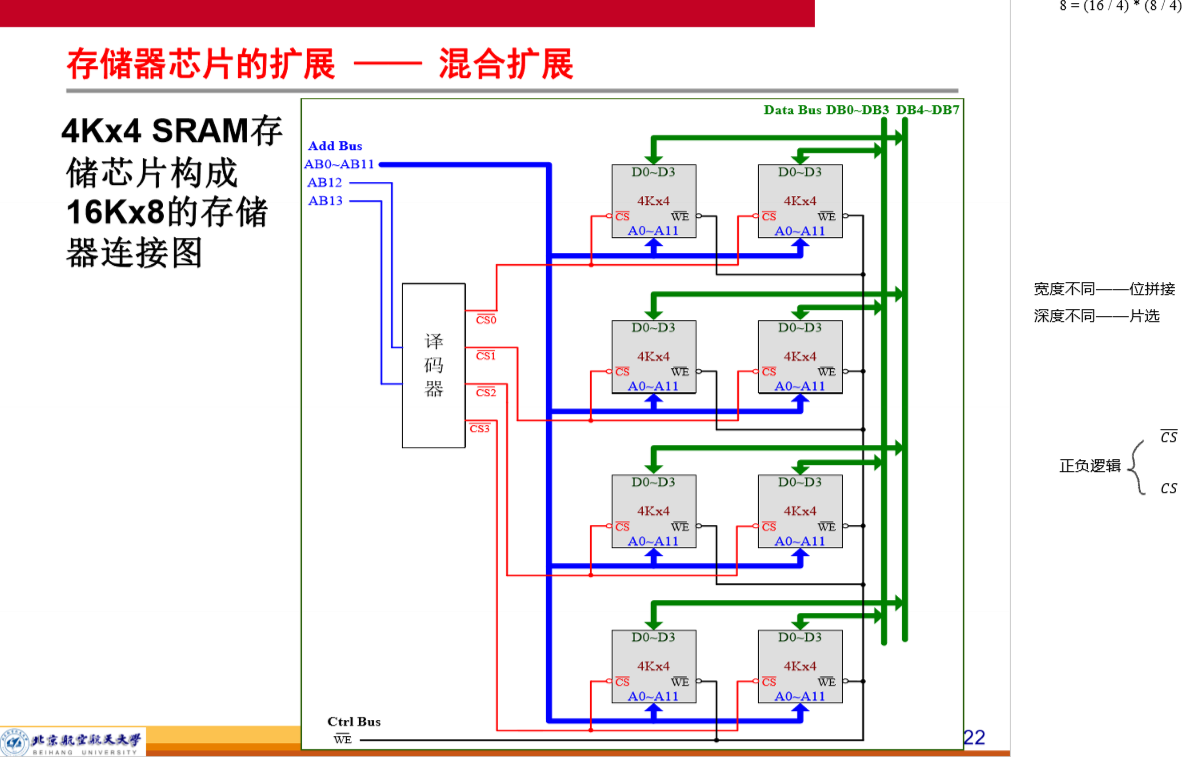
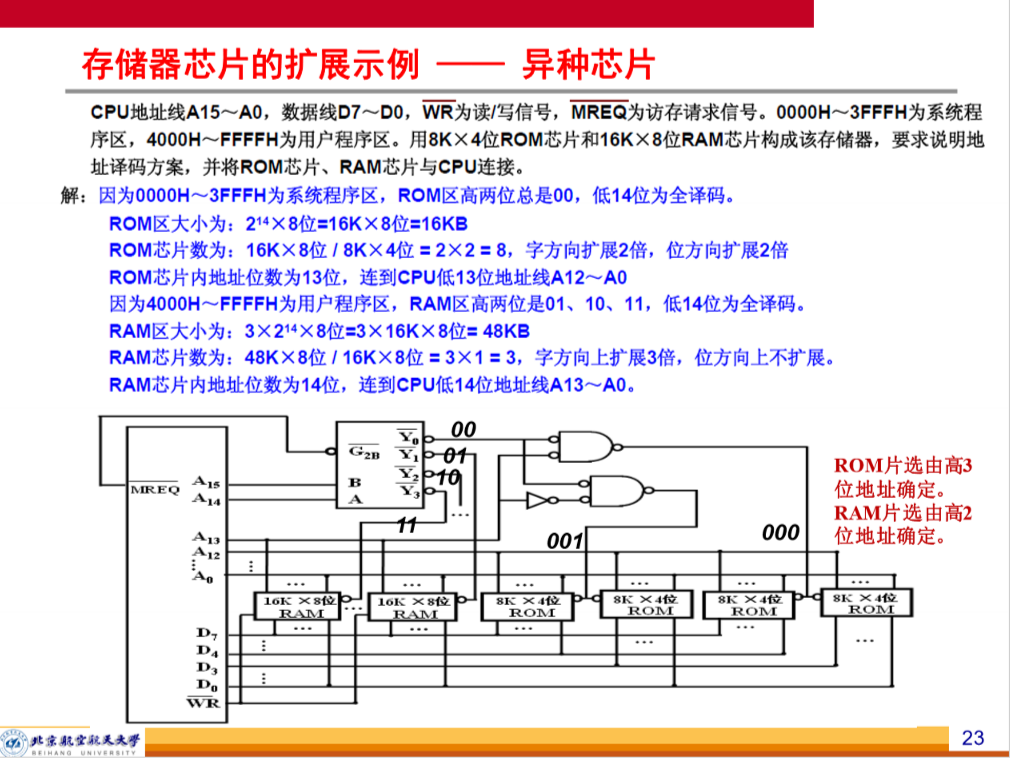
DRAM 的刷新
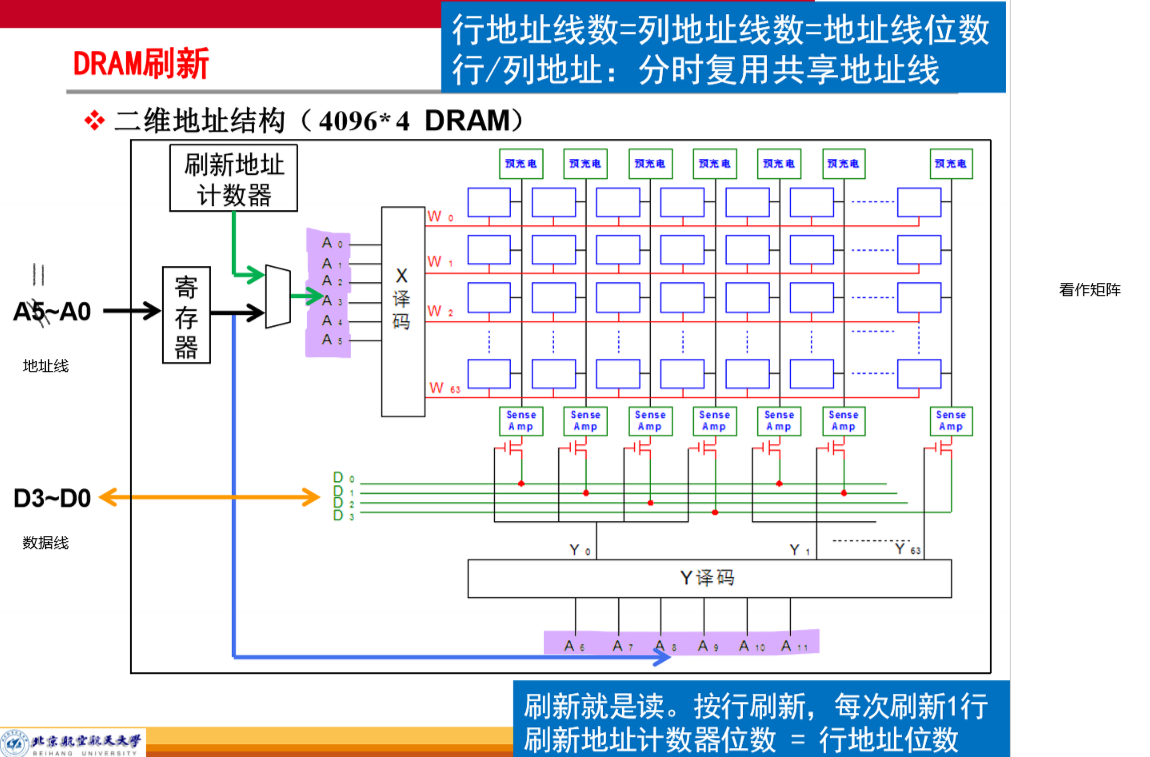

指令系统与 MIPS 汇编语言
指令系统概述
指令系统的基本要素
指令格式

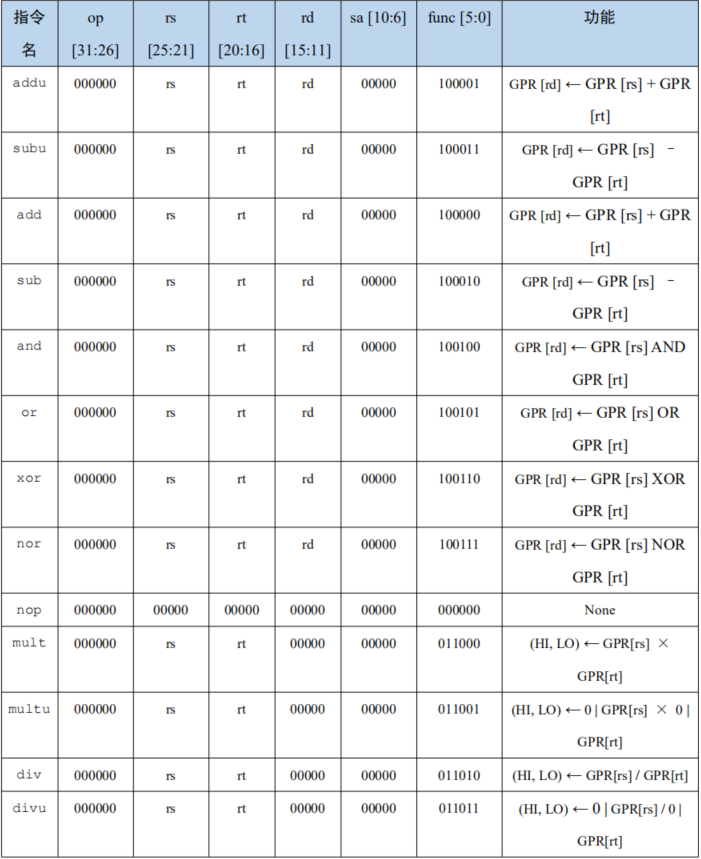
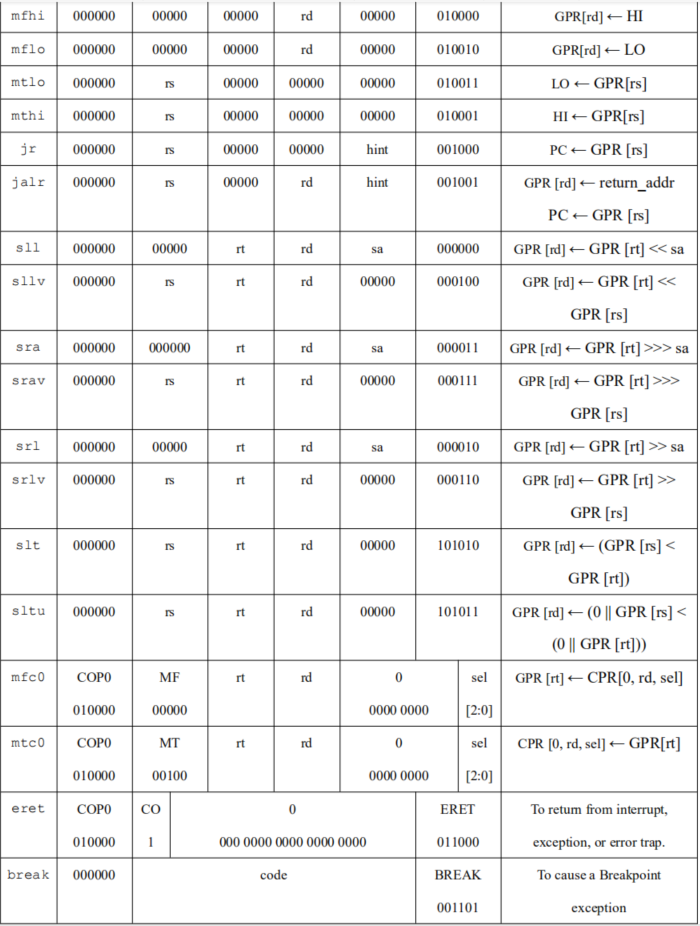
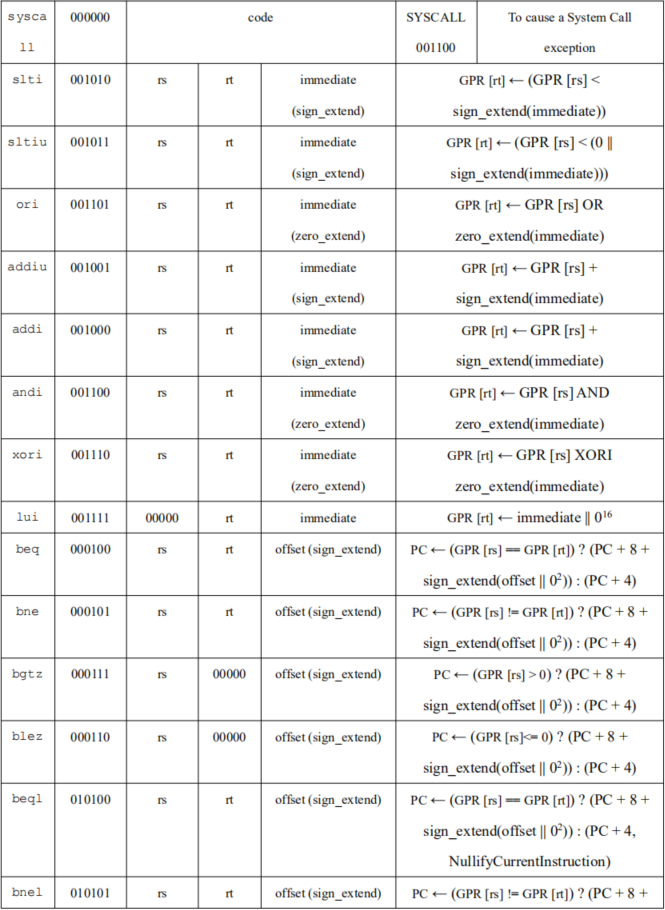 !
!
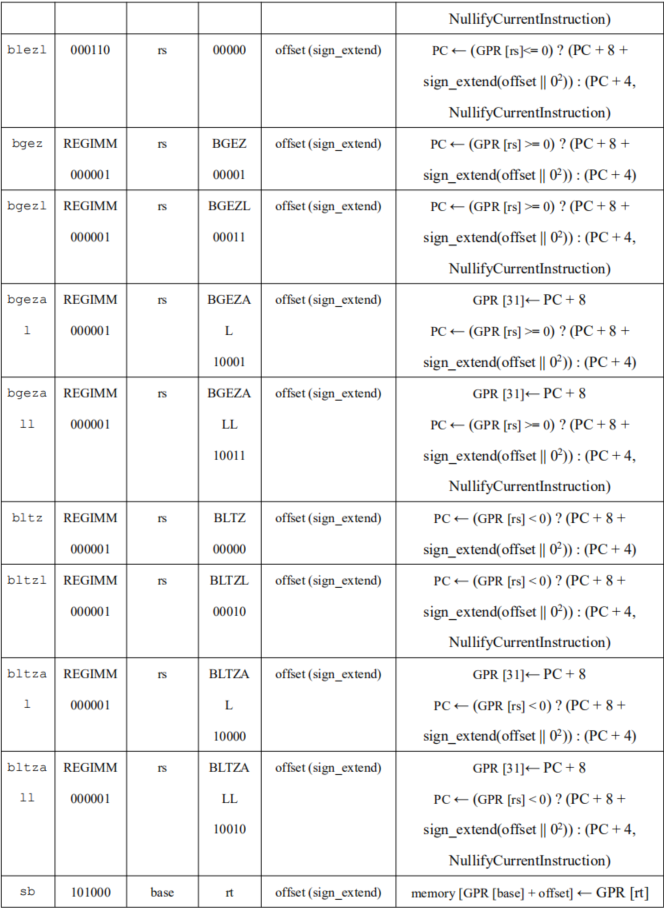
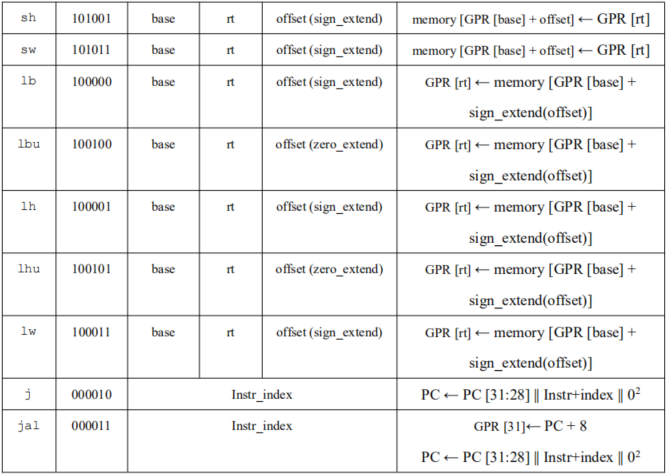
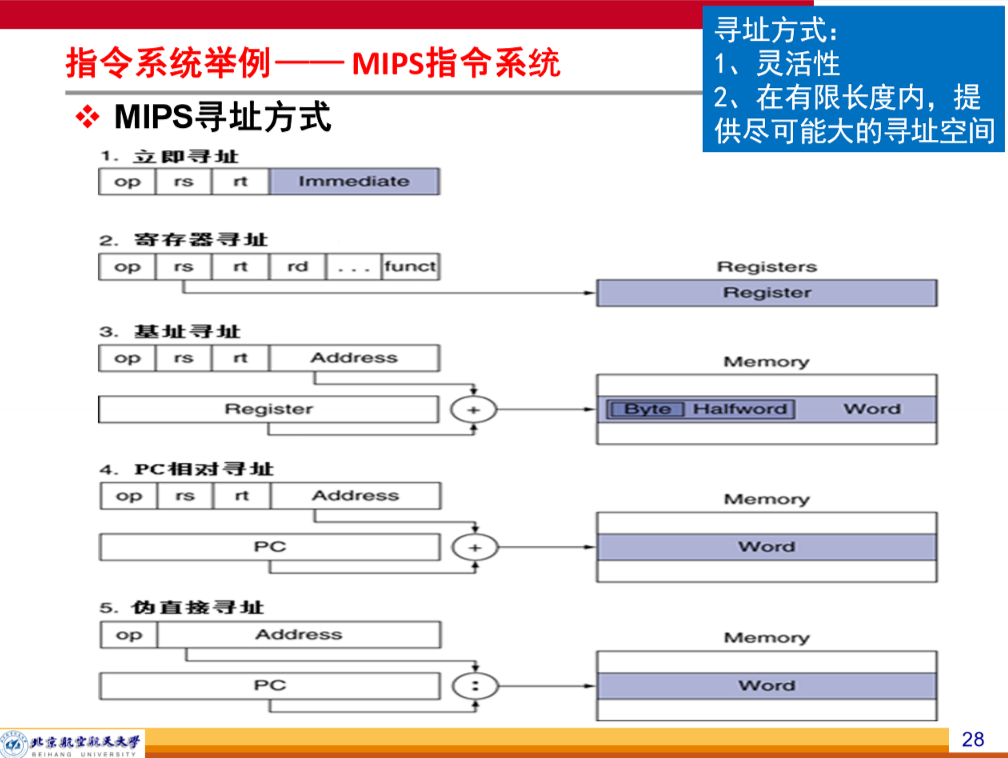
MIPS 指令系统


MIPS 汇编语言编程
MIPS 处理器设计
处理器的功能、组成、一般设计方法等
MIPS 处理器设计概述
结构、指令集、数据通路的基本组件
单周期处理器设计

单周期数据通路和控制器设计

单周期处理器性能分析
流水线处理器设计
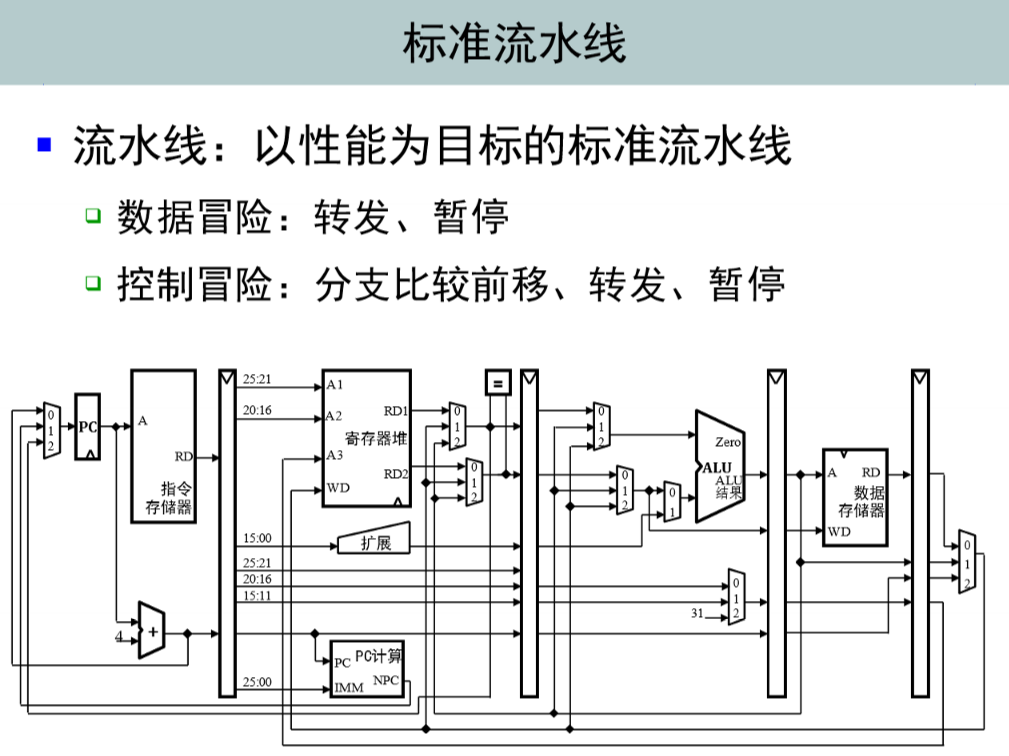

流水线数据通路和控制器设计
流水线处理器性能分析
流水线冒险及其处理
高速缓冲存储器 (Cache)
程序执行局部性原理
时间局部性
空间局部性
局部性成因
- 绝大多数情况下指令顺序执行
- 程序主要行为特征表现为循环
- 数组、结构等具有局部性
存储层次常用概念
-
数据包含原则:高层次数据 $\in$ 低层次数据
-
数据交换基本原则:数据交换一般只在相邻两层之间完成
-
命中 Hit
-
命中率 Hite Rate (HR)
-
缺失 Miss
-
缺失率 Miss Rate (MR)
HR + MR = 1
-
命中时间 Hit Time (HT):包括查找时间、判断时间以及数据读写时间的总和
-
缺失代价 Miss Penalty (MP):某层缺失后从下层获取数据所需要的时间。
Cache 的结构与工作原理
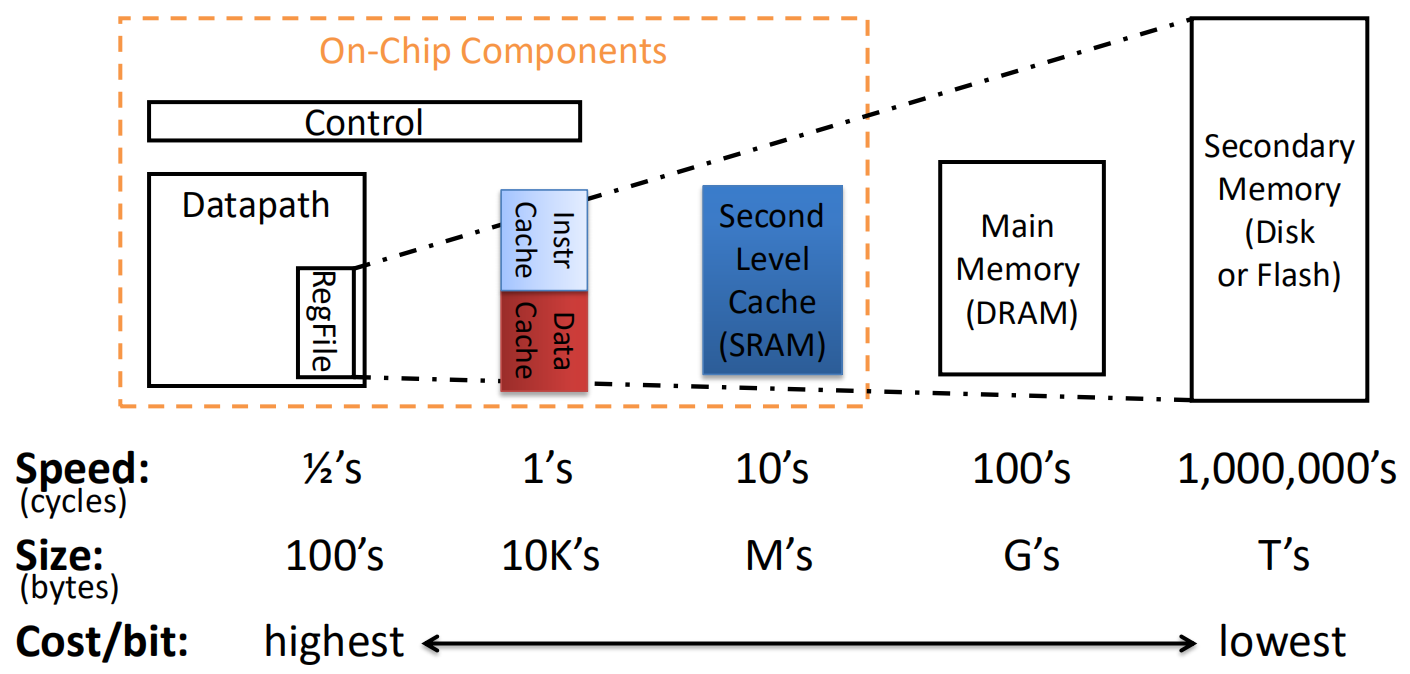
cache 的每个数据单元被称为块(cache block)
寄存器与 cache 之间的数据交换以 寄存器 为单位,但 cache 之间以及 cache 与下层主存储器之间的数据交换以 cache 块为单位。
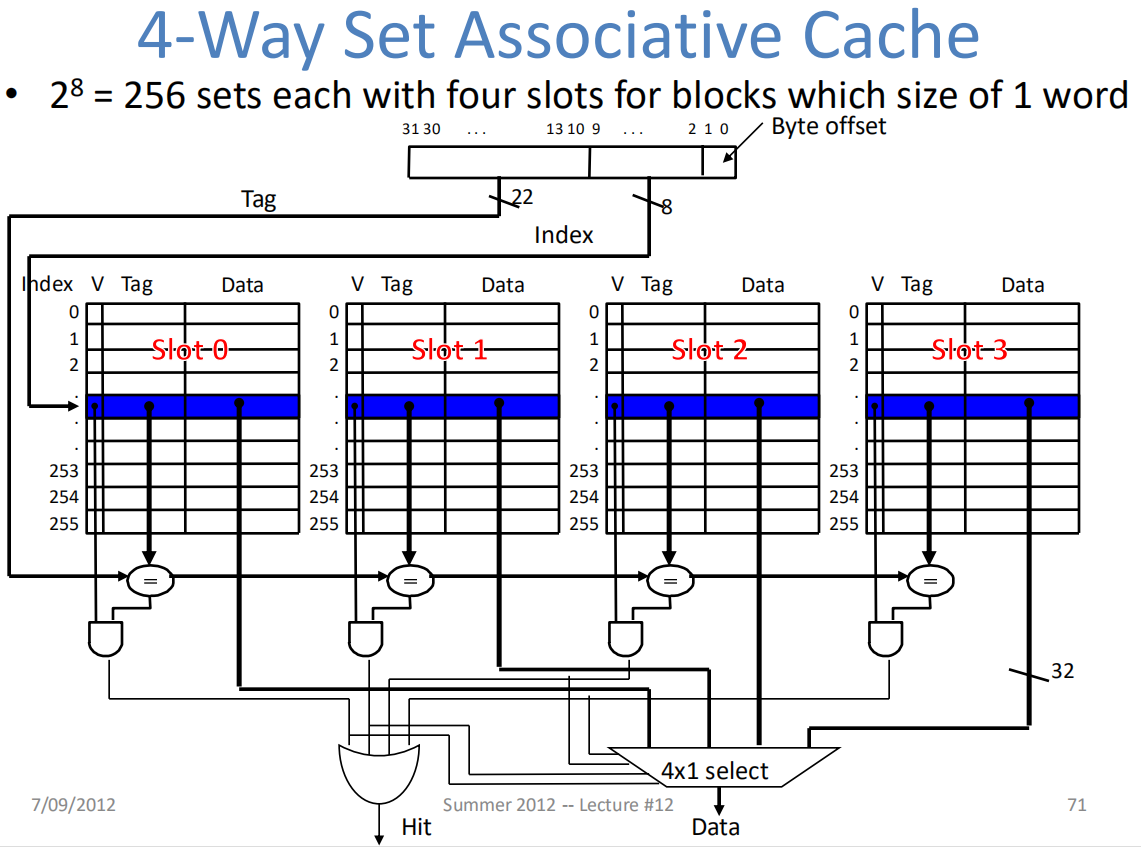
Cache 的映射机制
直接映射 Direct-Mapped Cache
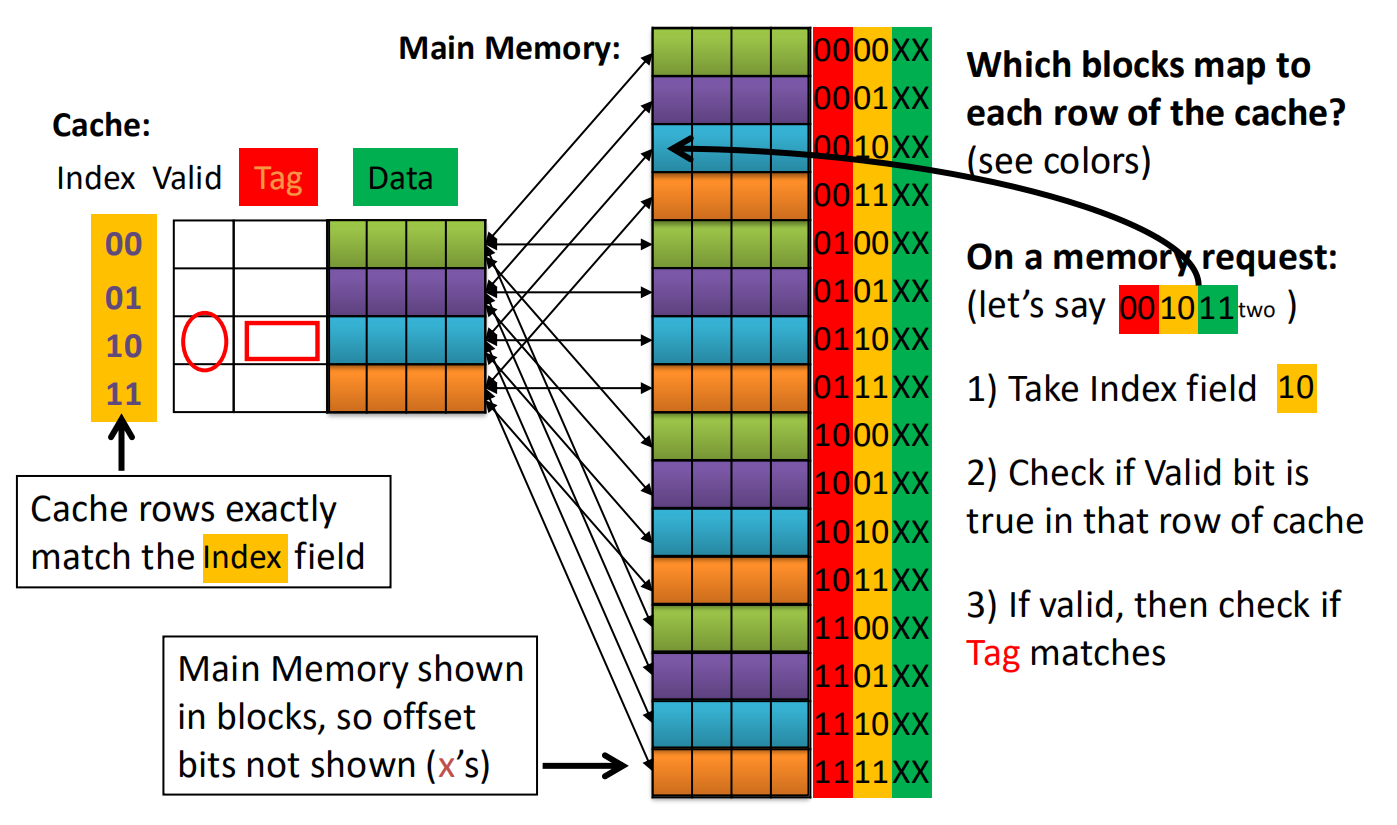
| 有效 | 标记 | 索引 | 块内偏移 |
|---|---|---|---|
Valid |
Tag |
Index |
Offset |
| $1$ | $地址总位数 - Offset - Index$ | $\log_2{cache块总数}$ | $\log_2{cache块大小}$ |
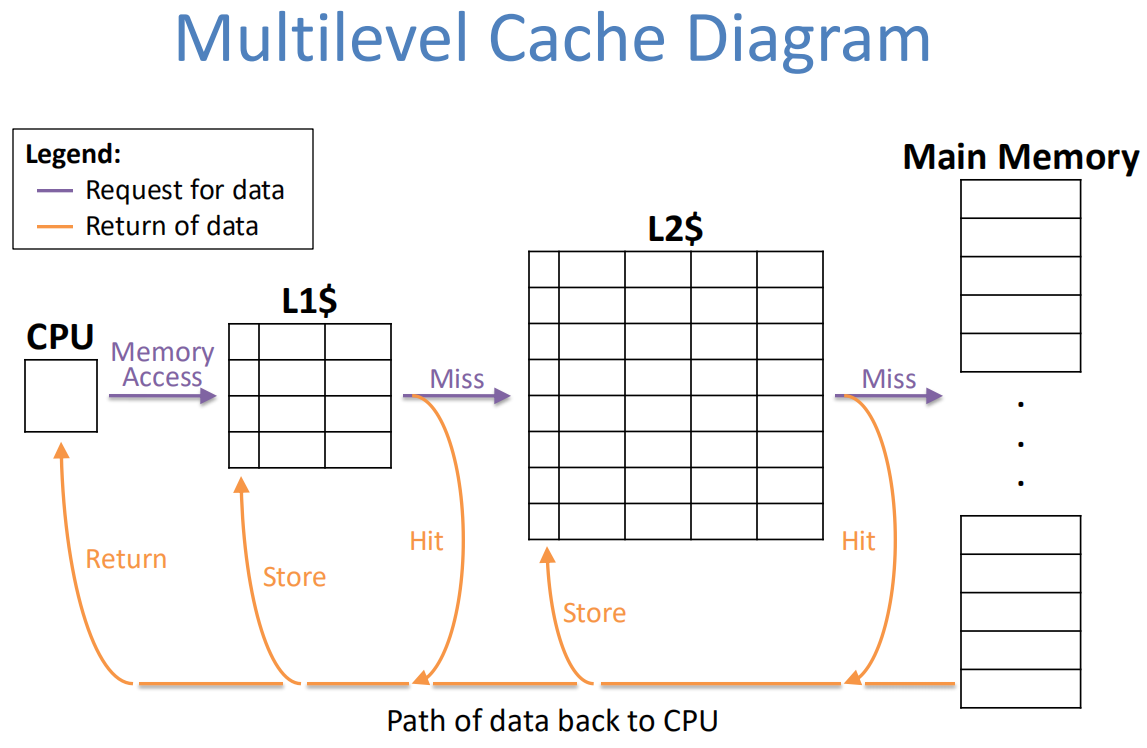
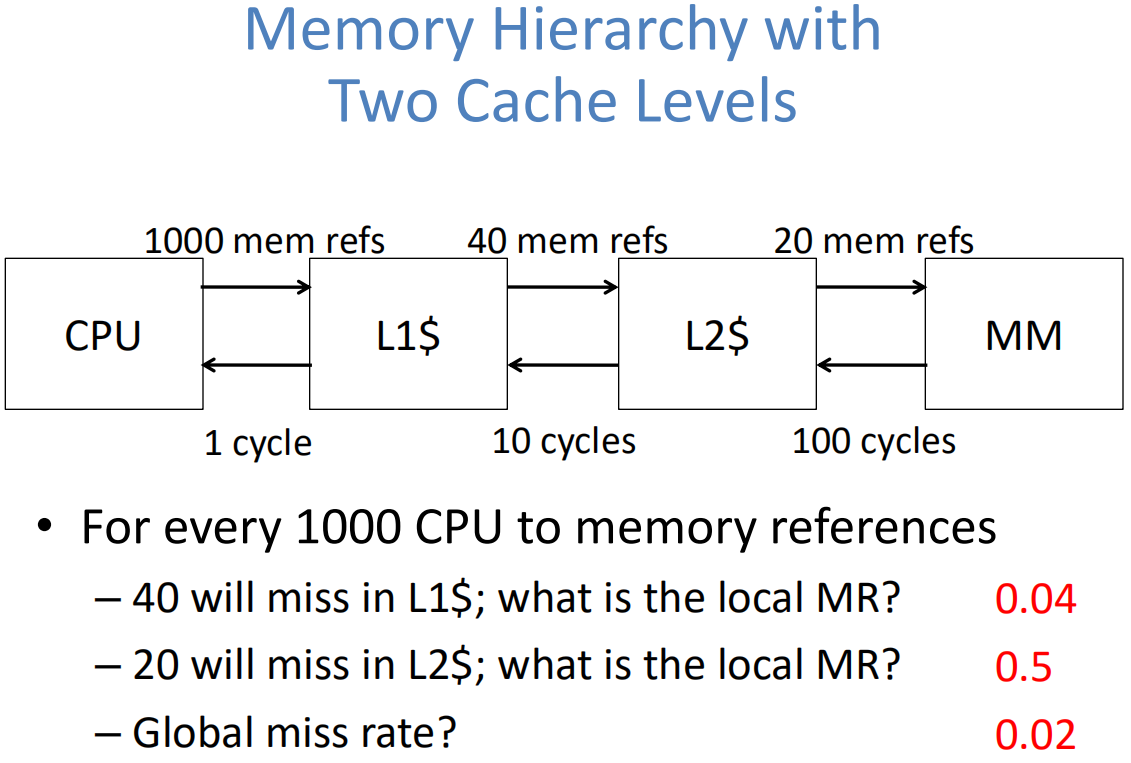
多级 Cache
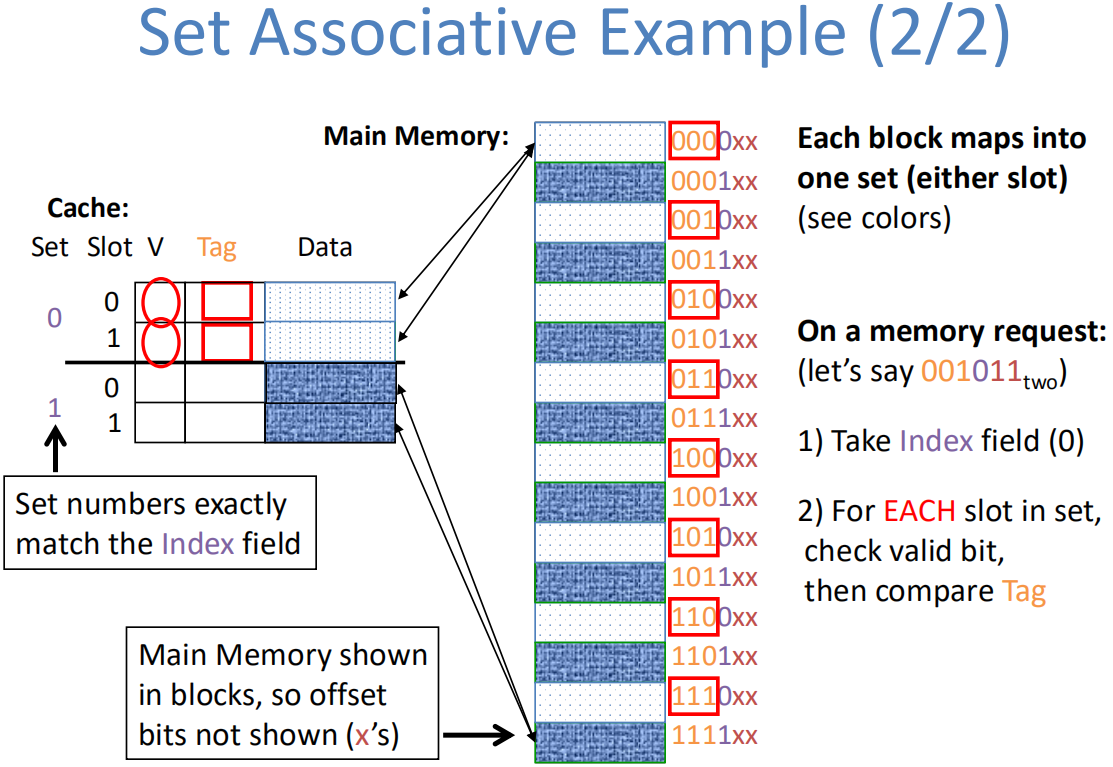
全相联映射
组相联映射





Cache 的替换策略
Cache 性能分析与其他
容量计算
性能分析
直接映射
AMAT (Average Memoory Access Time)
average time to access memory considering both hits and misses.
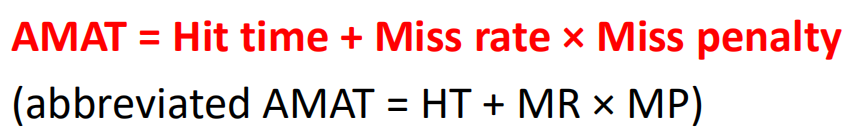






多级 Cache





组相联映射
Cache 数据一致性问题
Write-Through Policy 写通

Write-Back Policy 写回

处理 Cache 缺失


改进 Cache 性能

