Paper Reading: A Neural Probabilistic Language Model

Bengio, Y., Ducharme, R., & Vincent, P. (2000). A neural probabilistic language model. Advances in neural information processing systems, 13.

Background

Research Problem

Statistical Language Modeling: learn the joint probability function of sequences of words

Research foundation

• A statistical model of language can be represented by the conditional probability of the next word given all the previous ones in the sequence, since $P(w_1^T) = \prod_{t=1}^TP(w_t

  w_1^{t-1})$, where $w_t$ is the $t$-th word, and writing subsequence $w_i^j = (w_i, w_{i+1},…,w_{j-1}, w_j)$

• Premise: temporally closer words in the word sequence are statistically more dependent.

Difficulty

The curse of dimensionality

e.g. If one wants to model the joint distribution of 10 consecutive words in a natural language with a vocabulary $V$ of size 100,000, there are potentially $100000^{10} - 1$ free parameters.

Related Work

Method	Drawback
n-gram	not taking into account contexts farther than 1 or 2 words not taking account of the similarity between words

A Neural Probabilistic Language Model

Fighting the Curse of Dimensionality with its Own Weapons

1. Associate with each word in the vocabulary a distributed “feature vector” (a real-valued vector in $\mathbb{R}^m$), thereby creating a notion of similarity between words.

   The number of features is much smaller than the size of the vocabulary. The idea of using a vector-space representation for words has been well exploited in the area of information retrieval

2. Express the joint probability function of word sequences in terms of the feature vectors of these words in the sequence.

   The probability function is expressed as a product of conditional probabilities of the next word given the previous ones. The probability function in the experiment is a multi-layer neural network The probability function is a smooth function of these feature values, so a small change in the features induces a small change in the probability.

3. Learn simultaneously the word feature vectors and the parameters of that function.

The Proposed Model: two Architectures

The training set

A sequence $w_1 … w_T$ of words $w_t\in V$

• $V$: vocabulary, a large but finite set

Objective

• Goal: learn a good model $f(w_t,…,w_{t-n})=\hat{P}(w_t

  w_1^{t-1})$

• Metric: the geometric average of $1/\hat{P}(w_t

  w_1^{t-1})$, also known as perplexity, which is also the exponential of the average negative log-likelihood.

• Constraint: for any choice of $w_1^{t-1}$, $\sum_{i=1}^{

  V

  }f(i, w_{t-1}, w_{t-n})=1$

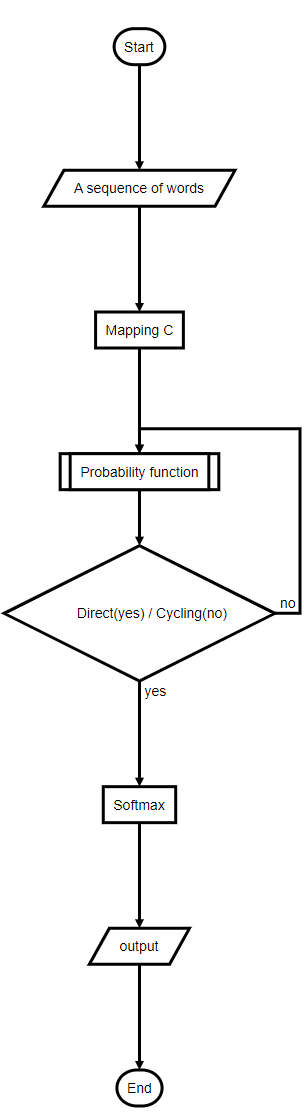
Basic Form

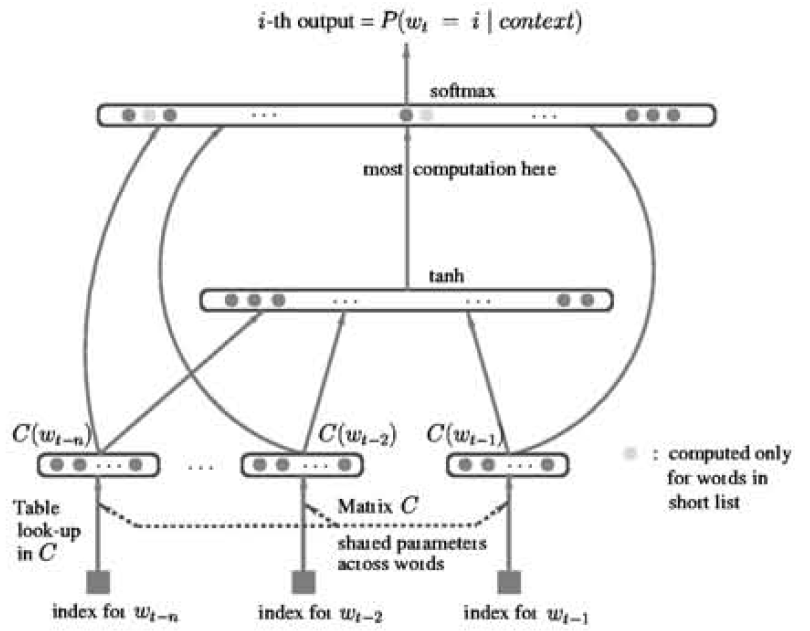
• Mapping $C$: a $

  V

  \times m$ matrix, converge any element of $V$ to a real vector $C(i)\in \mathbb{R}$.

  • shared parameters across all words in the context
• Probability function $f$
  • The direct architecture
    • a function $g$ maps a sequence of feature vectors for words in context $(C(w_{t-n}),…,C(w_{t-1}))$ to a probability distribution over words in $V$.

    • it’s a vector function whose $i$-th element estimates the probability $\hat{P}(w_t=i

      w_1^{t-1})$

    • use softmax in the output layer of a neural net: $\hat{P}(w_t=i

      w_1^{t-1})=e^{h_i}/\sum_j e^{h_j}$, where $h_i$ is the neural network output score for word $i$

  • The cycling architecture
    • a function $h$ maps a sequence of feature vectors for words in context $(C(w_{t-n}),…,C(w_{t-1}), C(i))$ to a probability distribution over words in $V$. (including the context words and a candidate next word $i$) to a scalar $h_i$
    • use softmax
    • each time putting in input the feature vector $C(i)$ for a candidate next word $i$

Fig. Direct Architecture

Speeding-up technique

Short list

Instead of computing the actual probability of the next word, the neural network is used to compute the relative probability of the next word within that short list.

The choice of the short list depends on the current context(the previous $n$ words). Used smoothed trigram model to pre-compute a short list containing the most probable next words associated to the previous two words.

Table look-up for recognition

To pre-compute in a hash table the output of the neural network

Stochastic gradient descent

Other tricks

Capacity control

Double-precision computation is very important to obtain good results.

Mixture of models

Initialization of word feature vectors

• random initialization
• SVD: Singular Value Decomposition

Out-of-vocabulary words

Take the average feature vector of all the words in the short list.

Experiments Result

• The neural network performs much better than the smoothed trigram
• More context is useful
• Hidden units help
• Learning the word features jointly is important
• Initialization not so useful
• Direct architecture works a bit better
• Conditional mixture helps but even without it the neural net is better