线性表

线性表的概念和表抽象数据类型

表的概念和性质

• 线性表

  一个（有穷或无穷）的基本元素集合 E, E 中一组有穷个元素排列成的序列 $L = (e_0, e_1, e_2, …,e_{n-1})$

• 下标

• 空表

• 长度

• 首元素 & 尾元素

  唯一

• 前驱元素

• 后继元素

表抽象数据类型

线性表的操作

表抽象数据类型

线性表的实现：基本考虑

1. 空间（计算机内存）
2. 时间（各种重要操作的效率）

顺序表的实现

顺序表——表中元素顺序存放在一片足够大的连续存储区内，首元素存入存储区开始位置，其余元素依次顺序存放，元素之间的逻辑顺序关系通过元素在存储区域里的物理位置表示。

基本实现方式

若顺序表中存储的元素类型相同，则：

• 存取操作可以在 O(1) 的时间内完成。
• 元素访问是 O(1) 复杂度的操作

若顺序表中元素大小不统一，则

• 可以将实际数据元素另行存储，在顺序表里各单元位置保存相应元素的引用信息（链接/索引）。

顺序表基本操作的实现

创建和访问操作

• 创建空表`

  创建新表的存储区后，应立即将两个表信息域(max 与 num) 设置好，保证这个表处于合法状态

• 简单判断操作 O(1)

  • 空表：num == 0
  • 表满：num == max

• 访问给定下标 i 的元素 O(1)

• 遍历操作 O(n)

• 查找给定元素 d 的（第一次出现的）位置 O(n)

• 查找给定元素 d 在位置 k 后第一次出现的位置 O(n)

变动操作：加入元素

• 尾端加入新数据项 O(1)

• 新数据存入元素存储区的第 i 个单元

  • 不要求维持原有元素的相对位置：O(1)

    将原有第 i 个单元的元素放入 num，再将新元素写入第 i 个单元

  • 要求保持原有元素的相对位置： O(n)

    把包括第 i 个单元的所有单元向后平移一位，再将新元素写入第 i 个单元

变动操作：删除元素

• 尾端删除数据 O(1)

• 删除位置 i 的数据

  • 软删除

    添加合法下标，再删除元素时将合法下标改为非法

  • 硬删除

    • 不需要保持原有顺序 O(1)

      将 num - 1 填入 i，再尾端删除

    • 需要保持原有顺序 O(n)

      将第 i 个删除，再将其后面的每个元素前移一位

• 基于条件的删除 O(n)

  基于条件：不直接给出删除元素的位置，而是给出需要删除数据项的条件

  需要通过循环实现，循环中逐个检查元素，查找到后将其删除。

顺序表及其操作的性质

顺序表优缺点总结：

• 优点：
  • O(1) 时间的（随机、直接的）按位置访问元素；
  • 元素在表里存储紧凑，除表中的存储区之外只需要 O(1) 空间存放少量的辅助信息
• 缺点：
  • 需要连续的存储区存放表中的元素，若表很大，则需要大片连续的内存空间。
  • 一旦确定了存储块的大小，可容纳单元个数并不随着插入 /删除操作的进行而变化。如果很大的存储区只保存了少量的数据项，就会有大量空闲单元，造成表内的存储浪费。
  • 另外，在执行加入或删除操作时，通常需要移动许多元素，效率低。
  • 最后，建立表需要考虑元素存储区大小，而实际需求通常很难事先估计。

Python 的 list

• 创建线性表

• lst = []

• 加入元素

  • 尾端加入单一元素：lst.append(x)
  • 将数据存入第 i 个单元：lst.insert(i, x)

• 删除元素

  • 删除尾端元素：lst.pop()
  • 删除下标为 i 的元素：lst.pop(i)
  • 删除第一个内容为 x 的元素：lst.remove(x)

• 求表长

  • len(lst)

• 清除 list 中的所有元素

  • lst.clear()

• 将 list 中的元素倒置

  • lst.reverse()

• 将 list 中的元素排序

  • sort：会修改 list 本身，不会返回新的 list
  • sorted：不会修改 list 本身，会返回排序好的 list

  lst = [3,4,5,1,2]
  print(lst.sort())   # None
  print(lst)          # [1,2,3,4,5]
  ######
  lst = [3,4,5,1,2] 
  print(sorted(lst))  # [1,2,3,4,5]
  print(lst)          # [3,4,5,1,2]
  

链接表（链表）

线性表的基本需要和链接表

链接表的基本思路：

• 把表中的元素分别存储在一批独立的存储块（称为表的结点）里
• 保证从组成表结构中的任一个节点可找到于其相关的下一个结点
• 在前一结点里用链接的方式显式地记录与下一个结点的关联

单向链接表（单链表）

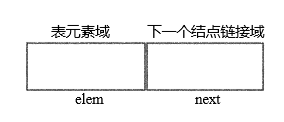
• 一个单链表由一些具体的表结点构成
• 每个结点是一个对象，由自己的标识，下面也常称其为该节点的链接
• 结点之间通过结点链接建立其单向顺序联系

# 定义一个简单的表结点类
class LNode:
    def __init__(self, elem, next_ = None):
        self.elem = elem
        self.next = next_ # 为了避免与 python 标准函数 next 重名

基本链表操作

创建空链表

把相应的表头变量设置为空连接

删除链表

将表指针赋值为 None

判断表是否为空

检查表头指针是否为 None

判断表是否满

一般链表不会满

加入元素

表首端插入

1. 创建一个新结点并存入数据
2. 把原链表首结点的链接存入新结点的链接域 next
3. 修改表头变量，使之指向新结点

q = LNode(13)
q.next = head
head = q

一般情况的元素插入

1. 创建一个新结点并存入数据
2. 把 pre 所指结点的 next 域的值存入新结点的链接域 next
3. 修改 pre 的 next 域，使之指向新结点

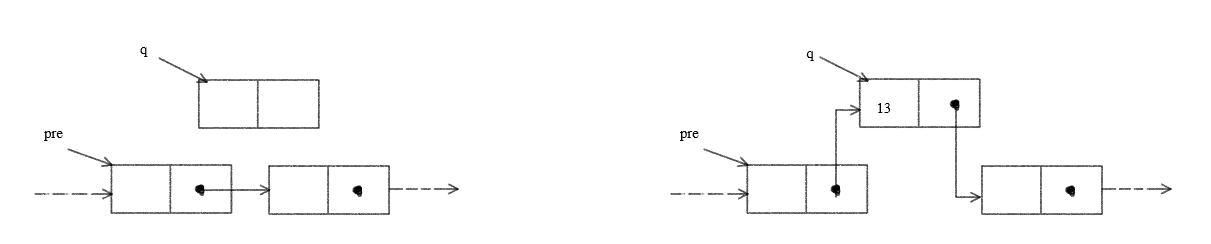
q = LNode(13)
q.next = pre.next
pre.next = q

删除元素

删除表首元素

修改表头指针，令其指向表中的第二个结点

head = head.next

一般情况的元素删除

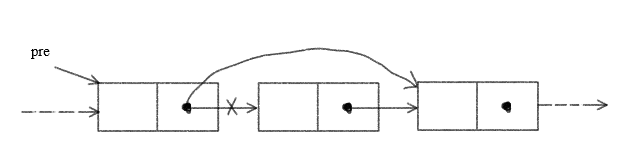
pre.next = pre.next.next

扫描、定位和遍历

p = head
while p is not None and 还需要继续的其它条件:
    对 p 所指结点里的数据做所需操作
    p = p.next

按下标定位

p = head
while p is not None and i > 0:
    i -= 1
    p = p.next

按元素定位

p = head
while p is not None and not pred(p.elem):
    p = p.next

遍历

p = head
while p is not None:
    p = p.next

链表操作的复杂度

操作	具体说明	复杂度
创建空表		O(1)
删除表		O(1)
判断空表		O(1)
加入元素	首端加入元素	O(1)
	尾端加入元素	O(n)
	定位加入元素	O(n)
删除元素	首端删除元素	O(1)
	尾端删除元素	O(n)
	定位删除元素	O(n)
	其它删除：通常需要扫描一整个表或者一部分	O(n)

求表的长度 O(n)

def length(head):
    p, n = head, 0
    while p is not None:
        n += 1
        p = p.next
    return n

链表的变形和操作

单链表的简单变形

在表对象中加入一个表尾引用域

循环单链表（循环链表）

最后一个结点的 next 域不用 None，而是指向表的第一个结点。

双向链接表（双链表）

节点之间由双向链接: prev, next

循环双链表

链表的排序

排序操作见后文“内部排序”

栈和队列

概述

栈、队列和数据使用顺序

栈 Stack

栈是保证元素后进先出（后存入先使用， Lat In First Out, LIFO） 关系的结构，简称 LIFO 结构。

队列 Queue

队列是保证元素先进先出（先存入者先使用，First In First Out, FIFO）关系的结构，简称 FIFO 结构。

应用环境

• 计算过程分为一些顺序执行的步骤
• 计算中执行的某些步骤会不断产生一些后面可能需要的中间数据
• 产生的数据中有些不能立即使用，但又需要在将来使用
• 需要保存的数据项数不能事先确定

栈：概念和实现

栈抽象数据类型

栈的线性表实现

• 对于顺序表，后端插入和删除都是 O(1) 操作，应该用这一端作为栈项（采用顺序表实现）
• 对于连接表，前端插入和删除都是 O(1) 操作，应该用这端作为栈项

栈的顺序表实现

采用 Python 的 list 数据结构

• 建立空栈：lst = []
• 压栈：lst.append()
• 弹栈：lst.pop()

栈的连接表实现

见前文连接表

栈的应用

数值转换

def Conversion(n, d): # 十进制数 n 转化为 d 进制数
    st = []
    while n > 0:
        st.append(n % d)
        n //= d
    while not st == []:
        print(st.pop(), end = "")
    print('')
    
# 试着运行一下
Conversion(8,2)

括号匹配问题

处理思路

• 顺序扫描被检查正文（一个字符串）中的每一个字符
• 检查中跳过无关字符（非括号字符）
• 遇到开括号”(“时将其压入栈
• 遇到闭括号时弹出当前的栈顶元素与之匹配
• 如果匹配成功则继续，发现不匹配时检查以失败结束

具体实现

def check_parens(text):
    """括号匹配检查函数，text 是被检查的正文串"""
    parens = "()[]{}" # 所有括号字符
    open_parens = "([{" # 开括号字符
    opposite = {")":"(", "]":"[", "}":"{"} # 表示匹配关系的字典
    
    def parentheses(text):
        """括号生成器，每次调用返回 text 里下一个括号及其位置"""
        i, text_len = 0, len(text)
        while True:
            while i < text_len and text[i] not in parens:
                i += 1
            if i >= text_len:
                return 
            yield text[i], i
            i += 1
            
    st = [] # 保存括号的栈
    for pr, i in parentheses(text): # 对 text 里各括号和位置迭代
        if pr in open_parens: # 开括号，压栈并继续
            st.append(pr)
        elif st == []: # 无法再弹栈
            return False
        elif st.pop() != opposite[pr]: # 不匹配就是失败，退出
            return False
        # else: 这是依次成功匹配，什么也不做，继续，因为上一步已经弹栈了
    if st == []:
        return True
    else:
        return False

# 应用一下试试看
re = check_parens("{(]")
if re:
    print("All parentheses are correctly matched.")
else:
    print("Parentheses mismatched.")

表达式的表示，计算和变换

表达式和计算的描述

• 中缀形式：(3 - 5) * (6 + 17 * 4) / 3

  中缀表达式表达能力最弱，只有在添加括号后才可达到相同的表达能力

• 前缀形式：/ * - 3 5 + 6 * 17 4 3

• 后缀形式：3 5 - 6 17 4 * + * 3 /

后缀表达式的计算

算法思路

• 遇到运算对象是，应该记录它以便后续使用
• 遇到运算符时，应该根据其元数（假定都是二元运算符），取得前面最近遇到的几个运算对象或已完成运算的结果，应用这个运算符计算，并保存其结果

注意事项

• 需要记录的是已经掌握的数据
• 每次处理运算符，应使用的是此前最后记录的几个结果

# 实现的伪代码如下：
# 假定 st 是一个栈，算法的核心是下面的循环
while 还有输入:
    x = nextItem() # 获取下一个输入
    if is_opend(x): # 如果是运算对象
        st.append(float(x))
    else: # 如果是运算符
        b = st.pop() # 第二个运算对象 ################################## 特别注意，先弹出来的是第二个运算数
        a = st.pop() # 第一个运算对象 ################################## 特别注意，后弹出来的是第一个运算数
        根据运算符对 a, b 进行运算
        st.append(c) #计算结果压入栈

def calculate(formula):
    formula = formula.split()
    st = [] # 栈
    for i in formula:
        if(i.isdigit()): # 若为数字
            st.append(int(i)) # 只支持整形运算
        else:
            b = st.pop() # 第二个运算数 ################################## 特别注意，先弹出来的是第二个运算数
            a = st.pop() # 第一个运算数 ################################## 特别注意，后弹出来的是第一个运算数
            if(i == '+'):
                c = a + b
            elif(i == '-'):
                c = a - b
            elif(i == '*'):
                c = a * b
            elif(i == '/'):
                c = a / b
            else:
                print("Illegal operator")
                return
            st.append(c)
    return st.pop()

# 试着运算看看
print(calculate("3 5 - 6 17 4 * + * 3 /"))

中缀表达式到后缀表达式的转换

• 扫描中遇到一个运算符不能将其输出，只要看到下一个运算符的优先级不高于本运算符的时候，才能够取做本运算符要求的计算
• 应该用一个栈保存尚未处理的运算符
• 需要处理括号问题
• 在扫描完成后，栈里可能剩下一些运算符，应将其一一弹出并送到后缀表达式。

中缀表达式的求值

栈与递归

阶乘函数的递归计算

栈与递归 / 函数调用

为了支持递归定义函数的实现，需要一个栈（运行栈）保存递归函数执行时每层调用的局部信息

队列

队列抽象数据类型

先进先出（First In First Out, FIFO）结构

• 入队（enqueue）
• 出队（dequeue）

队列的链接表实现

需要使用尾端指针

队列的顺序表实现

• 初始化 front = rear = 0
• 入队：将新元素插入 rear 所指向的位置，然后 rear 加一
• 出队：删去 front 所指的元素，然后加 1 并返回被删元素
• 队列为空：front = rear
• 队满：rear = MAX_QUEUE_SIZE - 1 或 front = rear

基于顺序表实现队列的困难

假溢出

在入队和出队操作中，头、尾指针只增加不减小，致使被删除元素的空间永远无法重新利用。因此，尽管队列中实际元素个数可能远远小于数组大小，但可能由于尾指针巳超出向量空间的上界而不能做入队操作。

循环顺序表（循环队列）

为循环队列所分配的空间可以被充分利用，除非向量空间真的被队列元素全部占用，否则不会上溢。

• q.elems —— 始终指向表元素区开始
• q.head —— 对头变量，记录当前队列里第一个元素的位置
• q.rear —— 队尾变量，记录当前队列里最后元素之后的第一个空位

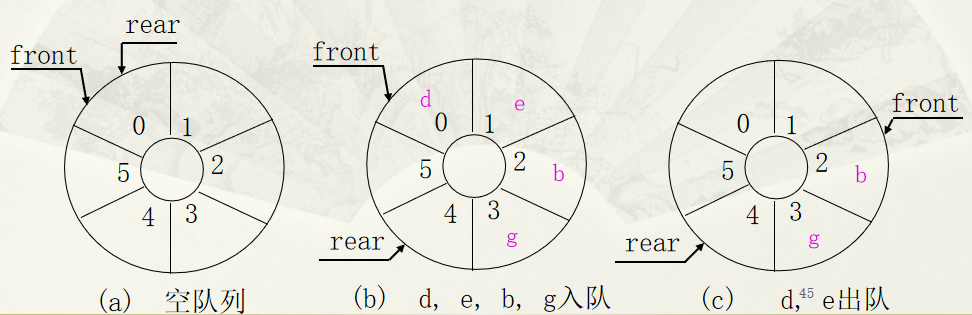
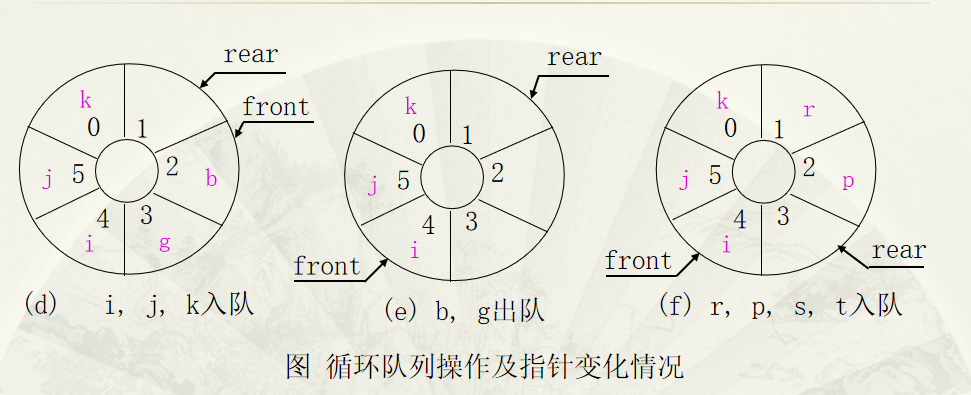
入队和出队分别需要更新变量 q.head 和 q.rear

• q.head = (q.head + 1) % q.len
• q.rear = (q.rear + 1) % q.len

队列的应用

BFS

串

字符集、字符串和字符串操作

字符串的相关概念

• 字符串长度

• 字符在字符串中的位置

• 字符串相等

• 字典序

• 字符串拼接

• 子串关系

  任何字符串也是该串自身的子串

• 前缀，后缀

字符串抽象数据类型

字符串的实现

基本实现问题和技术

实际语言里的字符串

Python 里的字符串

str 的操作

• 切分操作 split

  string.split('x')

  • 默认在空格处切分
  • 返回切分后的 list，其中每个元素不包含 ‘x’
  • 不改变原有字符串

• 替换操作 replace

  string.replace('a', 'b')

  • 一次替换掉全部满足要求的元素
  • 返回替换后的结果
  • 不改变原有字符串

• 检查子串出现的次数 count

  TimesOccured = string.count('x', start(, end))

• 检查后缀 endswith

  string.endswith('Ending')

  • 返回 Ture 或 False

• 找子串的位置 find/index

  string.find("substring", start(, end))

  string.index("substring", start(, end))

  • index() 方法检测字符串中是否包含子字符串 str ，该方法与 python find()方法一样，只不过如果 str 不在 string 中会报一个异常。

字符串匹配（子串查找）string matching

字符串匹配

假设有两个串（其中 $t_i, p_i$ 是字符）

$t = t_0t_1t_2…t_{n-1}$

$p = p_0p_1p_2…p_{m-1}$

在 $t$ 中查找与 $p$ 相同的子串

• 目标串：$t$
• 模式串：$p$

通常有 m « n, 即模式串长度远小于目标串长度

实际的串匹配问题

串匹配和朴素匹配算法

串匹配算法

朴素的串匹配算法 Brute Force

acdsgsdshvdncxmcudiwdnskxjzxjkxnvzbcshdiquso
dsh
acdsgsdshvdncxmcudiwdnskxjzxjkxnvzbcshdiquso
 dsh
acdsgsdshvdncxmcudiwdnskxjzxjkxnvzbcshdiquso
  dsh
acdsgsdshvdncxmcudiwdnskxjzxjkxnvzbcshdiquso
   dsh
acdsgsdshvdncxmcudiwdnskxjzxjkxnvzbcshdiquso
    dsh
acdsgsdshvdncxmcudiwdnskxjzxjkxnvzbcshdiquso
     dsh
acdsgsdshvdncxmcudiwdnskxjzxjkxnvzbcshdiquso
      dsh

无回溯串匹配算法（KMP 算法）

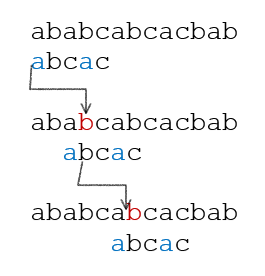
基本考虑

问题分析

当 $p_i$ 匹配失败时，所有的 $p_k(0\le k < i)$ 都已经匹配成功 。因此，只需要根据模式串 $p$ 本身即可决定匹配失败时如何前移。

对 $p$ 中的每个 $i$，都有与之对应的下标 $k_i$，与之匹配的目标串无关。（$k_i$ 课通过对于模式串 $p$ 的预分析得到）假设模式串 $p$ 的长度为 $m$，则需要对每个 $i(0\le i<m)$ 计算出对应的 $k_i$ 并将其保存起来，以便在匹配中使用。为此可以考虑一个长为 $m$ 的表 pnext，用表元素 pnext[i] 记录与 $i$ 对应的 $k_i$ 值。

KMP 算法 O(n)

def matching_KMP(t, p, pnext):
    """KMP 串匹配，主函数"""
    j, i = 0, 0
    n, m = len(t), len(p)
    while j < n and i < m: # i == m 说明找到了匹配
        if i == -1 or t[j] == p[i]: # 考虑 p 中下一个字符
            j, i = j + 1, i + 1
        else: # 失败！考虑 pnext 决定的下一字符
            i = pnext[i]
    if i == m: # 找到匹配，返回其下标
        return j-1
    return -1 # 无匹配，返回特殊值

构造 pnext 表：分析

• 模式串移动之后，作为下一个用于匹配的字符的新位置，其前缀子串应该与匹配失败的字符串之前同样长度的子串相同。
• 如果匹配在模式串的位置 i 失败时，二位置 i 的前缀子串中满足上述条件的位置不止一处，那么只可能做最短的移动，将模式串移到最近的那个满足上述条件的位置，以保证不遗漏可能的匹配。
• 如果 $p_0…p_{i-1}$ 的最长相等前后缀的长度为 $k(0\le k<i-1)$，在 $p_i\not=t_j$ 时，模式串就应该右移 $i-k$ 位，即应把 pnext[i] 设置为 $k$

递推计算最长相等前后缀的长度

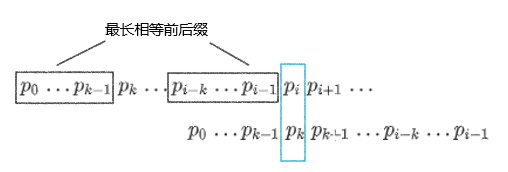
已知 pnext[0] = -1 和直至 pnext[i-1] 的已有值求 pnext[i] 的算法：

1. 假设 pnext[i-1] = k-1。如果 $p_i = p_k$，那么 $p_0…p_i$ 的最长相等前后缀的长度就是 $k$，将其计入 pnext[i]，将 $i$ 的值加一后继续递推（循环）
2. 如果 $p_i\not=p_k$，就将 $k$ 设置为 pnext[k] 的值
3. 如果 $k$ 的值等于 -1（这个值一定是第 2 步而来自 pnext），那么 $p_0…p_i$ 的最长相同前后缀的长度就是 0，设置 pnext[i] = 0，将 $i$ 的值加 1 后继续递推。

pnext 生成算法的改进

def gen_pnext(p):
    """生成针对 p 中各位置 i 的下一个检查位置表，用于 KMP 算法，有稍许修改的优化版本"""
    i, k, m = 0, -1, len(p)
    pnext = [-1] * m
    while i < m-1: # 生成下一个 pnext 元素
        if k == -1 or p[i] == p[k]:
            i, k = i + 1, k + 1
            if p[i] == p[k]:
                pnext[i] = pnext[k]
            else:
                pnext[i] = k
        else:
            k = pnext[k]
    return pnext

KMP 算法的时间复杂性及其它

• 构造 pnext O(m)
• 实际匹配 O(n)
• 综上： O(m+n)

数组

数组

数组的定义

数组的抽象数据类型定义

数组的顺序表示和实现

一般采用顺序存储的方法来表示数组

行优先顺序（Row Major Order）

$a_{11}\ a_{12}\ …\ a_{1n}\ a_{21}\ a_{22}\ …\ a_{2n}\ …\ a_{m1}\ a_{m2}\ …\ a_{mn}$

列优先顺序（Column Major Order）

$a_{11}\ a_{21}\ …\ a_{m1}\ a_{12}\ a_{22}\ …\ a_{m2}\ …\ a_{1n}\ a_{2n}\ …\ a_{mn}$

不同存储方式的地址计算

矩阵的压缩存储

对于高阶矩阵，若其中非零元素呈某种规律分布或者矩阵中有大量的零元素，则考虑压缩存储

• 多个相同的非零元素只分配一个存储空间
• 零元素不分配空间

特殊矩阵

是指非零元素或零元素的分布有一定规律的矩阵。

对称矩阵

对称矩阵中的元素关于主对角线对称，因此，让每一对对称元素$a_{ij}$和$a_{ji}, (i\not=j)$分配一个存储空间，则$n^2$个元素压缩存储到$n(n+1)\over2$个存储空间，能节约近一半的存储空间。

三角矩阵

三角矩阵中的重复元素c可共享一个存储空间，其余的元素正好有$n(n+1)\over2$个，因此，三角矩阵可压缩存储到向量sa[$0…{n(n+1)\over2}$]中，其中c存放在向量的第1个分量中。

对角矩阵

矩阵中，除了主对角线和主对角线上或下方若干条对角线上的元素之外，其余元素皆为零。

对角矩阵可按行优先顺序或对角线顺序，将其压缩存储到一个向量中，并且也能找到每个非零元素和向量下标的对应关系。

稀疏矩阵 Sparse Matrix

稀疏矩阵的压缩存储

对于稀疏矩阵，采用压缩存储方法时，只存储非0元素。必须存储非0元素的行下标值、列下标值、元素值。因此，一个三元组$(i,\ j,\ a_{ij})$唯一确定稀疏矩阵的一个非零元素。

三元组顺序表

若以行序为主序，稀疏矩阵中所有非0元素的三元组，就可以得构成该稀疏矩阵的一个三元组顺序表。

求转置矩阵

1. 将矩阵的行、列下标值交换。即将三元组表中的行、列位置值i 、j相互交换；
2. 重排三元组表中元素的顺序。即交换后仍然是按行优先顺序排序的。

• 方法一：

  • 算法思想：

    按稀疏矩阵A的三元组表a.data中的列次序依次找到相应的三元组存入b.data中。

  • 算法分析：

    时间复杂度为$O(c_n\times t_n)$，即矩阵的列数和非0元素的个数的乘积成正比。

• 方法二：（快速转置）

  • 算法思想：

    直接按照稀疏矩阵A的三元组表a.data的次序依次顺序转换，并将转换后的三元组放置于三元组表b.data的恰当位置。

  • 前提：

    若能预先确定原矩阵A中每一列的(即B中每一行)第一个非0元素在b.data中应有的位置，则在作转置时就可直接放在b.data中恰当的位置。因此，应先求得A中每一列的非0元素个数。

  • 附设两个辅助向量num[ ]和cpot[ ] 。

    • num[col]：统计A中第col列中非0元素的个数；
    • cpot[col] ：指示A中第一个非0元素在b.data中的恰当位置。

稀疏矩阵的乘法

• 算法思想：

  对于A中的每个元素a.data[p](p=1, 2, … , a.tn)，找到B中所有满足条件：a.data[p].col=b.data[q].row 的元素b.data[q]，求得a.data[p].value * b.data[q].value，该乘积是$c_{ij}$中的一部分。求得所有这样的乘积并累加求和就能得到$c_{ij}$。

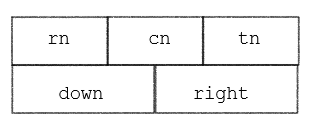
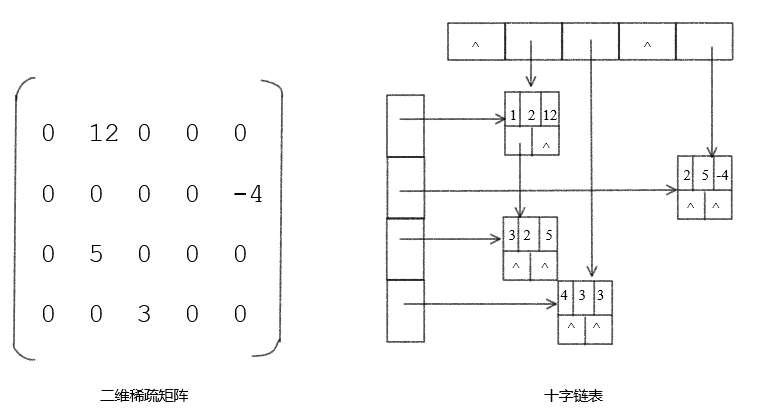
十字链表

矩阵非零元素结点所含有的域有：行、列、值、行指针（指向同一行的下一个非零元）、列指针（指向同一列的下一个非零元）

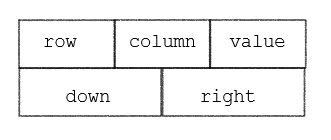
由定义知，稀疏矩阵中同一行的非0元素的由right指针域链接成一个行链表， 由down指针域链接成一个列链表。则每个非0元素既是某个行链表中的一个结点，同时又是某个列链表中的一个结点，所有的非0元素构成一个十字交叉的链表。称为十字链表。

其次，十字交叉链表还有一个头结点，结点的结构如图所示。

广义表 List

广义表是线性表的推广和扩充

广义表的概念

广义表是由 $n(n\ge 0)$ 个元素组成的有穷序列：$Lst = (a_1, a_2, … a_n)$

其中 $a_i$ 或者是原子项（不可再分），或者是一个广义表

• 表头

• 表尾

• 表深

  括号的最大层数

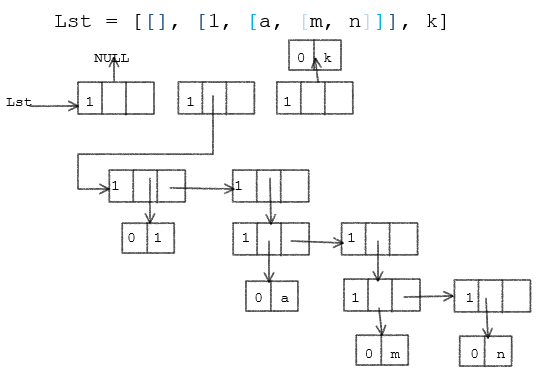
广义表的存储结构

由于广义表中的数据元素具有不同的结构，通常用链式存储结构表示，每个数据元素用一个结点表示。因此，广义表中就有两类结点：

• 表结点：

  用来表示广义表项，由标志域，表头指针域，表尾指针域组成

• 原子结点：

  用来表示原子项，由标志域，原子的值域组成

树

树形结构是由结点（结构中的逻辑单元，可用于保存数据）和结点之间的连接关系（一种后继关系）构成，其结构域线性结构（表）不同，主要特征有：

• 一个结构如果不空，其中就存在着唯一的起始点，称为树根(root)
• 一个结点有且只有一个前驱，可以有 0 个或者多个后继
• 结构里的所有结点都在树根结点通过后继关系可达的结点集合里
• 结点之间的联系不会构成循环关系
• 从任意俩能够不同的结点出发，通过后继关系可达的两个结点的集合，或者互不相交，或者一个为另一个的子集。

二叉树：概念和性质

概念和性质

定义和图示

• 二叉树
• 左子树
• 右子树
• 空树
• 单点树
• 子节点
• 父节点
• 树叶
• 度数——一个结点的子节点个数

路径、结点的层和树的高度

二叉树的性质

满二叉树、扩充二叉树

• 满二叉树：二叉树中所有分支结点的度数都是 2
• 扩充二叉树：将二叉树扩充为满二叉树，新增加的结点称为外部结点，原有结点称为内部结点。

完全二叉树

对于一棵高为 $h$ 的二叉树，如果其第 $0$ 层到第 $h-1$ 层的结点都满，最下一层的结点不满，且所有结点在最左边联系排列，空位都在右边。

抽象数据类型

遍历二叉树

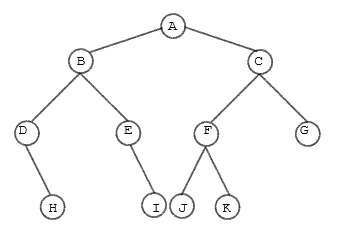
A B C D E F G None H None I J K

深度优先遍历 (DFS)

• 先根序遍历（DLR）$\rightarrow$ 先根序列

  A B D H E I C F J K G

• 中根序遍历（LDR），也称对称序 $\rightarrow$ 中根序列

  D H B E I A J F K C G

• 后根序遍历（LRD）$\rightarrow$ 后根序列

  H D I E B J K F G C A

宽度优先遍历 (BFS)

按层次顺序遍历

A B C D E F G H I J K

遍历与搜索

二叉树的 list 实现

设计和实现

• 空树用 None 表示

• 非空二叉树用包含桑元素的表[d, l, r] 表示，其中：

  • d 表示存在根节点的元素
  • l 和 r 是两棵子树

• 表示样例：

  ['A', ['B', None, None],
        ['C', ['D', ['F', None, None],
                    ['G', None, None],
               'E', ['H', None, None],
                    ['I', None, None]]]]
  

二叉树的 class 实现与遍历

树类型定义

class TreeNode(object):
    def __init__(self, value, left, right):
        self.value = None
        self.left = None
        self.right = None

根据层序输入生成树

def CreateTree(root, tree):
    """根据层序输入生成树"""
    queue = []
    queue.append(root)
    global i
    while(i < len(tree)):
        t = queue[0]
        t.value = tree[i]
        queue.pop(0)
        t.left = TreeNode(None, None, None)
        t.right = TreeNode(None, None, None)
        queue.append(t.left)
        queue.append(t.right)
        i += 1

递归遍历

递归前序遍历

def presearch(root):
    """递归——前序遍历"""
    if not root:
        return None
    else:
        if not(root.value == "None" or root.value == None):
            print(root.value, end = " ")
        presearch(root.left)
        presearch(root.right)

递归中序遍历

def midsearch(root):
    """递归——中序遍历"""
    if not root:
        return None
    else:        
        midsearch(root.left)
        if not(root.value == "None" or root.value == None):
            print(root.value, end = " ")
        midsearch(root.right)

递归后序遍历

def postsearch(root):
    """递归——后序遍历"""
    if not root:
        return None
    else:        
        postsearch(root.left)        
        postsearch(root.right)
        if not(root.value == "None" or root.value == None):
            print(root.value, end = " ")

非递归遍历

非递归前序遍历

代码

def nonrec_presearch(root):
    """非递归——前序遍历"""
    dlr = []
    stk = [] # 栈空间
    now = root
    while not(now == None or now.value == None or now.value == "None") and (len(stk) == 0)):
        elif now == None or now.value == None or now.value == "None":
            now = stk.pop()
        else:
            dlr.append(now.value)
            stk.append(now.right)
            now = now.left  
    # 打印出遍历结果
    print(dlr)

算法思想

while 当前结点不为空 or 栈空间不为空时:
    if 当前结点为空:
        当前结点 = stack.pop()
    else:
        1. 先访问当前结点（根节点）
        2. 右子节点进栈
        3. 当前结点设置为左子节点

非递归中序遍历

代码

def nonrec_midsearch(root):
    """非递归——中序遍历"""
    ldr = []
    stk = [] # 栈空间
    now = root
    while not ((now.value == None or now.value == "None") and (len(stk) == 0)):
        if now.value == None or now.value == "None":
            now = stk.pop()
            ldr.append(now.value)
            now = now.right
        else:
            stk.append(now)
            now = now.left
    # 打印出遍历结果
    print(ldr)

算法思想

while 当前结点不为空 or 栈空间不为空时:
    if 当前结点为空:
        当前结点 = stack.pop()
        访问当前节点
        当前结点设置为右子节点
    else:
        stack.push(当前节点)
        当前结点设置为左子节点

非递归后序遍历

代码

def nonrec_postsearch(root):
    """非递归——后序遍历"""
    lrd = []
    stk = [] # 栈空间
    now = [root, 0]
    while not ((now[0].value == None or now[0].value == "None" or now[0] == None) and (len(stk) == 0)):
        if now[0].value == None or now[0].value == "None" or now[0] == None:
            now = stk.pop()
            now[1] += 1
        elif now[1] == 0:
            stk.append(now)
            now = [now[0].left,0]
        elif now[1] == 1:
            stk.append(now)
            now = [now[0].right,0]
        elif len(stk) == 0:
            lrd.append(now[0].value)
            break
        else:
            lrd.append(now[0].value)
            now = stk.pop()
            now[1] += 1
    # 打印出遍历结果
    print(lrd)

算法思想

需要引入"计数"，即是否可以访问根节点
计数为 0: now = now.left
   为 1: now = now.right
   为 2: 访问当前结点

树的存储

树、森林与二叉树的转换

霍夫曼树的构造

设有实数集 $W = {w_0, w_1, …, w_{m-1}},\ T$ 是一棵扩充二叉树，其 m 个外部节点分别以 $w_i(i = 1,2,…,n-1)$ 为权，且 T 的带权外部路径长度 WPL 在所有这样的扩充二叉树中达到最小，则称 T 为 W 的最优二叉树或哈夫曼树。

图

概念、性质与实现

定义与图示

• 有向图
• 无向图

概念与性质

• 完全图：任意两个顶点之间都有边的图
• 度：一个顶点的度就是与它邻接边的条数。
  • 入度
  • 出度

路径的相关性质

• 路径的长度：该路径上边的条数
• 回路
• 简单回路：一个环路，除起点和终点外其它顶点均不相同
• 简单路径：内部不包含回路的路径
• 有根图：在有向图里存在一个顶点 v，到其它每个顶点均有路径

连通图

• 连通
• 连通无向图：任意两个顶点之间都连通
• 强 连通有向图：任意两个顶点之间都有路径（要求两个方向的路径都存在）

子图、连通子图

• 极大连通子图
• 极大强连通子图

带权图和网络

• 带权图
• 网络

图抽象数据类型

图的表示和实现

邻接矩阵

$A_{ij} = \left{ \begin{array}{lr} 1, 如果顶点 v_i 到 v_j 有边 \ 0，如果顶点 v_i 到 v_j 无边\end{array}\right.$

图的邻接表表示

对图的每个顶点建立一个单链表，存储该顶点所有邻接顶点及其相关信息。每一个单链表设一个表头结点。

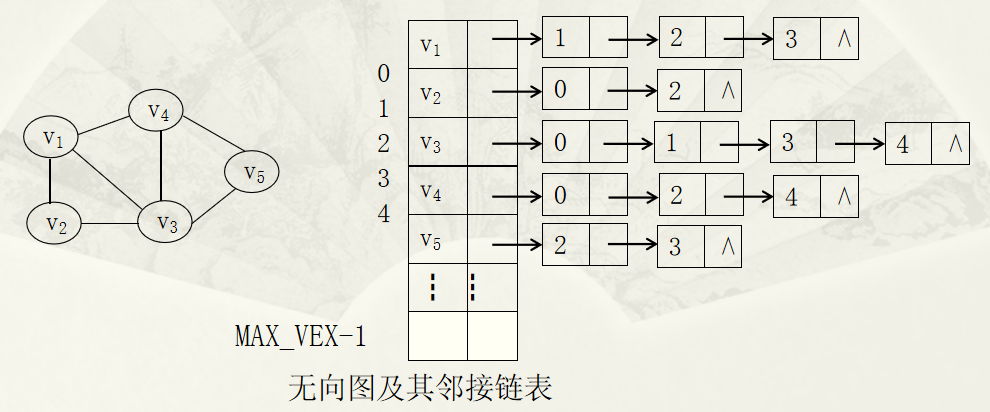
图的 Python 实现

用字典实现

• 字典的声明：

  Graph = dict()

• 使用：

  Graph[key] = value

由输入构造树

# get input
NodeNum, PathNum, Start, End = input().split()
NodeNum = int(NodeNum)
PathNum = int(PathNum)
Start = int(Start)
End = int(End)
# Create Graph
Graph = dict()
for i in range(NodeNum):
    Graph[i+1] = dict()
for i in range(PathNum):
    temp = input().split()
    Graph[int(temp[0])][int(temp[1])] = int(temp[2])

图的遍历

深度优先遍历

宽度优先遍历

生成树

条件：连通无向图 或 强连通有向图

如果图 G 有 n 个顶点，必然可以找到 G 中的一个包含 n-1 条边的集合，这个集合里包含了从 $v_0$ 到其它所有点的路径。

遍历和生成树

构造 DFS 生成树

构造 BFS 生成树

最小生成树

最小生成树问题

最小生成树 —— 带权树中权值最小的生成树

Kruskal 算法

算法思路

将图看作离散的点和一堆边
dot = []
while num(边) < n - 1:
    从未选择的边中找到满足：<m ,n>
    1. 权重最小
    2. 两个端点不同时出现在已连接的点中
    dot.append(m)
    dot.append(n)
    将边从未选择中删除
    num(边) ++

![img](https://upload-images.jianshu.io/upload_images/3755117-2656ffcd5cdb097d.png?imageMogr2/auto-orient/strip

imageView2/2/w/1200/format/webp)

![img](https://upload-images.jianshu.io/upload_images/3755117-8392698e3388fece.png?imageMogr2/auto-orient/strip

imageView2/2/w/1200/format/webp)

Prim 算法

![img](https://upload-images.jianshu.io/upload_images/3755117-4491cf0d977af08c.png?imageMogr2/auto-orient/strip

imageView2/2/w/1200/format/webp)

![img](https://upload-images.jianshu.io/upload_images/3755117-ac654c5400c4a97e.png?imageMogr2/auto-orient/strip

imageView2/2/w/1200/format/webp)

最短路径

最短路径问题

求单原点最短路径的 Dijikstra 算法

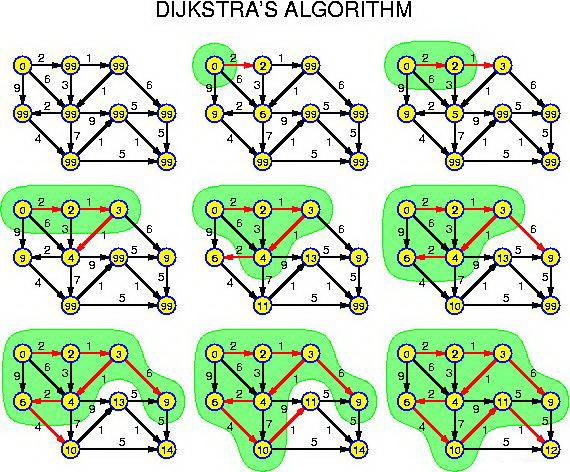
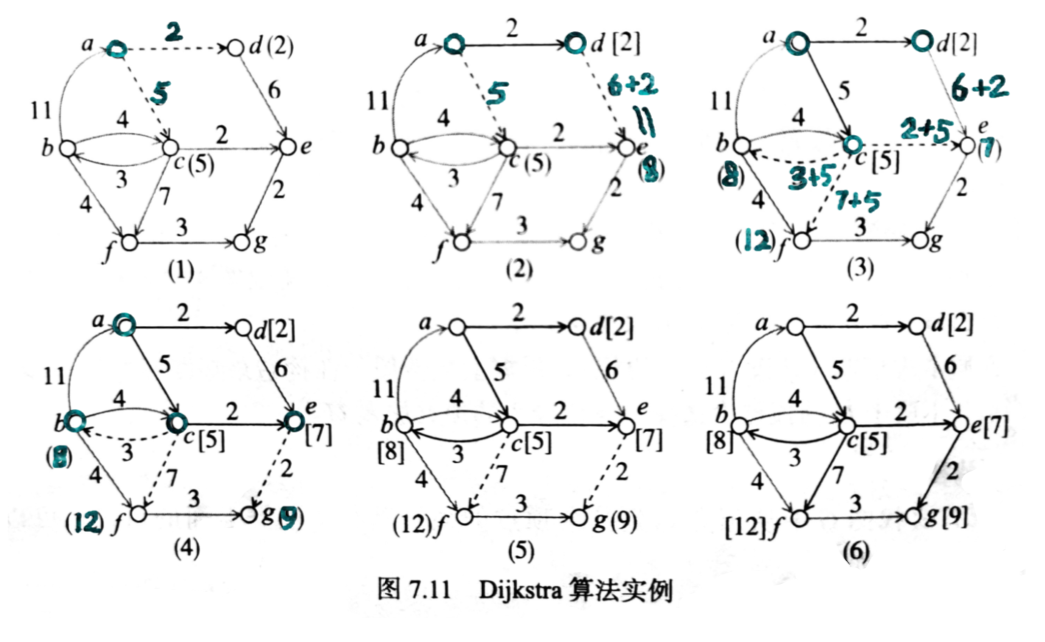
# FindPath
Path[Start] = (Start,0)
for i in Graph[Start]:
    CanReach.append((Graph[Start][i],i,Start))
while(len(Arrive) < NodeNum):
    CanReach = sorted(CanReach)
    i = 0
    while(CanReach[i][1] in Arrive):
        i += 1
    at = CanReach[i][1]
    length = CanReach[i][0]
    Arrive.append(at)
    Path[at] = ((CanReach[i][2], CanReach[i][0]))
    for j in Graph[at]:
        if(j not in Arrive):
            CanReach.append((length + Graph[at][j],j,at))

求任意顶点间的最短路径的 Floyd 算法

基于图的邻接矩阵表示

1. 若不允许经过任何中间点，则最短路径就是邻接矩阵
2. 允许经过第一个顶点，与邻接矩阵比较，算出最小值
3. 允许经过第一个和第二个顶点，…
4. …

def Floyd(graph):
    N = len(graph)
    for i in range(N): # pass point i
        for m in range(N):
            for n in range(N): #<m, n>
                old = graph[m][n]
                new = graph[m][i] + graph[i][n]
                if(new < old):
                    graph[m][n] = new
    return graph

inf = 1000
Graph = [[0,2,6,4],
         [inf,0,3,inf],
         [7,inf,0,1],
         [5,inf,12,0]]
print(Floyd(Graph))

AOV / AOE 网及其算法

AOV 网，又称顶点活动网(activity on vertex network)，表示各项活动之间的先后顺序关系

AOV 网、拓扑排序和拓扑序列

拓扑排序和拓扑序列

拓扑排序 $S$：如果 $N$ 中存在顶点 $v_i$ 到 $v_j$ 的路径，那么 $S$ 里 $v_i$ 就排在 $v_j$ 之前

拓扑序列不唯一

拓扑序列不包含回路

拓扑排序算法

算法思路

1. 从 $N$ 中选出一个入度为 0 的顶点作为序列的下一顶点
2. 从 $N$ 网中删除所选顶点及其所有的出边
3. 反复执行上述步骤，直至已经选出了所有图中的顶点

代码

# get input
temp = input().split()
NodeNum = int(temp[0])
PathNum = int(temp[1])
Start = int(temp[2])
End = int(temp[3])
# Create Graph
Graph = dict()
ReGraph = dict()
From = dict()
EE = dict()
LE = dict()
Topology = [Start]
for i in range(NodeNum):
    Graph[i+1] = dict()
    From[i+1] = []
    ReGraph[i+1] = dict()
# Find Topology Order
now = Start
while not(now == End):
    for i in From:
        if now in From[i]:
            From[i].remove(now)
        if ((len(From[i]) == 0) and not (i in Topology)):
            Next = i
    Topology.append(Next)
    now = Next

AOE 网和关键路径

AOE 网 (Activity On Edge Network) 是另一类带权有向图

抽象来看，AOE 网是一种无环带权有向图，其中：

• 顶点表示事件，有向边表示活动，边上的权值表示活动的持续时间
• 图中一个顶点表示的事件，也就是它的入边所表示的活动都已完成，它的出边活动可以开始的那个状态。
• AOE 网中描述的活动可以并行地执行。

关键路径：完成整个工程所需的最短时间，就是从开始顶点到完成顶点的最长路径的长度。

关键路径算法

定义变量

• 事件 $v_j$ 最早可能发生时间 $ee[j]$
  • ee[0] = 0（初始时间总是在 0 时刻发生）
  • ee[j] = max{ee[i] + w[i, j]}
• 事件 $v_j$ 最迟允许发生时间 $le[j]$
  • 根据已知 ee[j] 反向推算
  • le[n - 1] = ee[n - 1] （最后一个事件绝不能再延迟）
  • le[i] = min{le[j] + w[i, j]}

定义概念

• 关键活动
  • ee[j] == le[j]
• 时间余量
  • t[j] = le[j] - ee[j]

关键路径：算法

1. 生成 AOE 网的一个拓扑序列
2. 按照拓扑正序，生成 ee 表的值
3. 按照拓扑逆序，生成 le 表的值
4. 将 e 与 l 一起计算，得到关键路径

import copy
def DFS(now, path):
    global Result, Critical, Graph, End
    if(now == End):
        Result.append(copy.copy(path))
        return
    for i in Graph[now]:
        if((i in Critical) and (Graph[path[-1]][i] == EE[i] - EE[path[-1]])):
            path.append(i)
            DFS(i, path)
            path.remove(i)
    return
# get input
temp = input().split()
NodeNum = int(temp[0])
PathNum = int(temp[1])
Start = int(temp[2])
End = int(temp[3])
# Create Graph
Graph = dict()
ReGraph = dict()
From = dict()
EE = dict()
LE = dict()
Topology = [Start]
for i in range(NodeNum):
    Graph[i+1] = dict()
    From[i+1] = []
    ReGraph[i+1] = dict()
for i in range(PathNum):
    temp = input().split()
    Graph[int(temp[0])][int(temp[1])] = int(temp[2])
    From[int(temp[1])].append(int(temp[0]))
    ReGraph[int(temp[1])][int(temp[0])] = int(temp[2])
print(Graph)
print(From)
# Find Topology Order
now = Start
while not(now == End):
    for i in From:
        if now in From[i]:
            From[i].remove(now)
        if ((len(From[i]) == 0) and not (i in Topology)):
            Next = i
    Topology.append(Next)
    now = Next
print(Topology)
# Find Critical Path
for i in Topology:
    if(i == Start):
        EE[Start] = 0
    else:
        can = []
        for j in ReGraph[i]:
            can.append(EE[j] + ReGraph[i][j])
        EE[i] = max(can)
print(EE)
Topology.reverse()
for i in Topology:
    if(i == End):
        LE[End] = EE[End]
    else:
        can = []
        for j in Graph[i]:
            can.append(LE[j] - Graph[i][j])
        LE[i] = min(can)
print(LE)
# Critical Path
Critical = []
for i in Graph:
    if(EE[i] == LE[i]):
        Critical.append(i)
Result = []
p = [Start]
DFS(Start, p)
Result = sorted(Result)
print(Result)

查找

顺序查找

从表的一端开始逐个将记录的关键字和给定K值进行比较，若某个记录的关键字和给定K值相等，查找成功；否则，若扫描完整个表，仍然没有找到相应的记录，则查找失败。

折半查找

折半查找又称为二分查找，是一种效率较高的查找方法。 前提条件：查找表中的所有记录是按关键字有序(升序或降序) 。 查找过程中，先确定待查找记录在表中的范围，然后逐步缩小范围(每次将待查记录所在区间缩小一半)，直到找到或找不到记录为止。

索引查找

分块查找(Blocking Search)又称索引顺序查找，是前面两种查找方法的综合。

索引树

B_树

一棵 m 阶 B 树或者为空，或者具有下面特征：

• 树中分支结点至多有 m-1 个排序存放的关键码。根结点至少有一个关键码，其他结点至少有 $\lfloor (m-1)/2\rfloor$ 个关键码
• 如果一个分支节点有 j 个关键码，它就有 j + 1 棵子树，这一结点中保存的是一个序列 $<p_0, k_0, p_1, k_1, …, p_{j-1}, k_{j-1}, p_j>$, 其中 $k_j$ 为关键码，$p_j$ 为子结点引用，而且 $k_i$ 大于 $p_i$ 所引子树里所有的关键码，小于 $p_{i+1}$ 所引子树里所有的关键码

B_ 树图文详解

B+树

B+ 树图文详解

平衡二叉树 AVL

定义和性质

平衡二叉排序树是一类特殊的二叉排序树，它或为孔数，或者其左右子树都是平衡二叉排序树，而且其左右子树的高度之差的绝对值不超过 1。

平衡因子 BF（Balance Factor）：该结点的左子树高度减去右子树高度之差，可能的取指只有 1, -1, 0

AVL 树类

如果能维持平衡二叉树的结构，检索操作就能在 $O(\log{n})$ 时间内完成

基本定义

为了实现 AVL 树，每个结点里需要增加一个平衡因子记录

插入操作

插入后的失衡与调整

• 不失衡的情况
  • 若在检索树的过程中，所有途径的结点 BF 均为 0，那么实际上插入结点也不会导致失衡
• 失衡的情况
  • 若失衡，则一定存在一棵包含实际插入点的最小非平衡子树，即包含新结点插入位置的、其根节点的 BF 非零的最小子树。如果插入新结点后这颗子树仍保持平衡，而且其高度不变，那么整棵二叉排序树也将保持平衡（由于该子树的高度不变，在它外面的树的结点的 BF 值都不变）。进一步说，如果插入新结点后的结构调整和 BF 值修改都能在子树内部的一条路径上完成，插入的复杂度将不超过 $O(\log{n})$
  • 类型
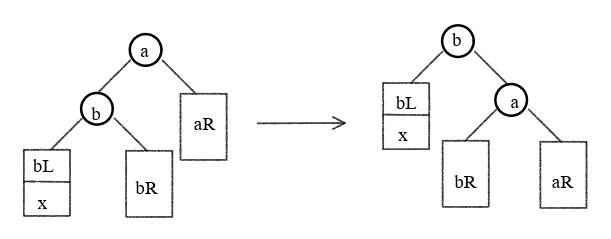
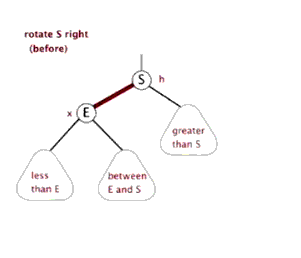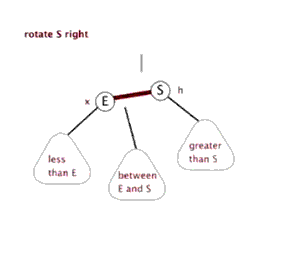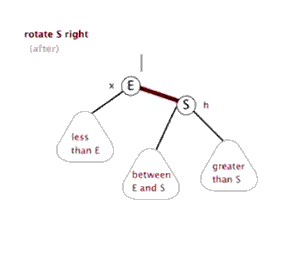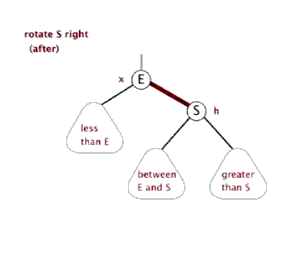
    • $LL$ 型调整【a 的左子树较高，新结点插入在 a 的左子树的左子树】
    • $LR$ 型调整【a 的左子树较高，新结点插入在 a 的左子树的右子树】
    • $RR$ 型调整【a 的右子树较高，新结点插入在 a 的左子树的右子树】
    • $RL$ 型调整【a 的右子树较高，新结点插入在 a 的左子树的左子树】
  • 在插入新结点并完成调整之后，这棵子树与插入之前这个位置上的子树高度相同，其结构变化对子树之外的部分无影响。

LL(RR) 失衡与调整

• LL

  

  

• RR

  

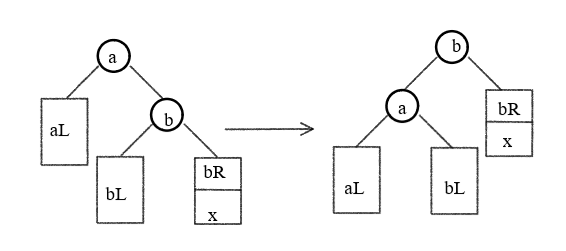
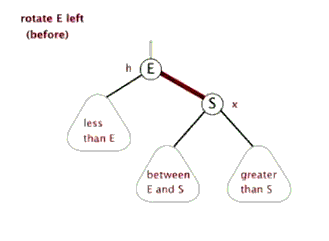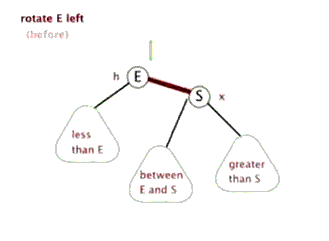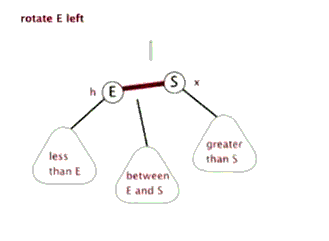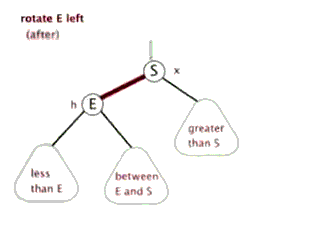
LR(RL) 失衡和调整

• LR

  

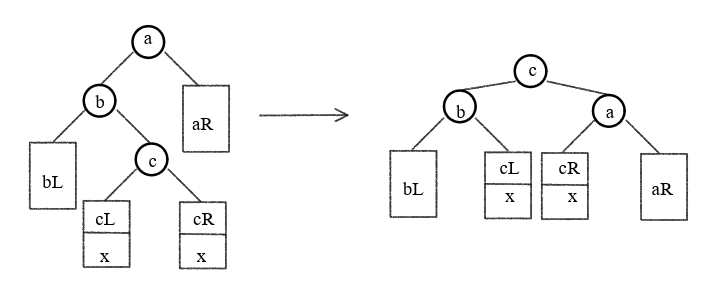
• RL

  

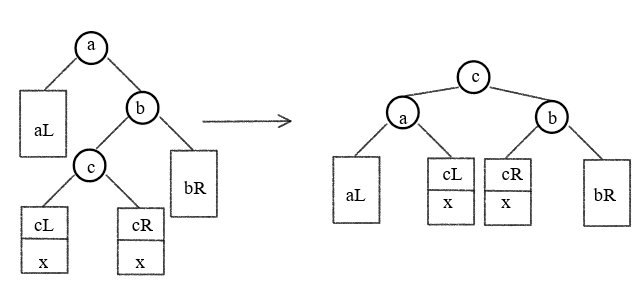
插入操作的实现

1. 查找新结点的插入位置，并在查找过程中记录遇到的最小不平衡子树的根
   • 用一个变量 a 记录距插入位置最近的平衡因子非零的结点，由于可能需要修改这棵子树，在此过程中用另一变量 pa 记录 a 的父结点
   • 如果不存在这种结点，需要考虑的 a 就是树根
   • 如果在新结点插入后出现失衡，a 就是平衡位置
   • 实际插入新结点
2. 修改从 a 的子结点到新结点的路径上各结点的平衡因子
   • 由于 a 的定义，这段结点原来都有 BF = 0
   • 插入后用一个扫描变量 p 从 a 的子结点开始遍历，如果新结点插入在 p 的左子树，就把 p 的平衡因子改为 1，否则改为 -1
3. 检查以 a 为根的子树是否失衡，失衡时做出调整
   • 如果 a.bf == 0，插入后不会失衡，简单修改平衡因子并结束
   • 如果 a.bf == 1，而且新结点插入其左子树，就出现了失衡
     • 新结点在 a 的左子节点的左子树时做 LL 调整
     • 新结点在 a 的右子节点的左子树时做 LR 调整
   • 如果 a.bf == -1，而且新结点插入其右子树，就出现了失衡
     • 新结点在 a 的左子节点的左子树时做 RL 调整
     • 新结点在 a 的右子节点的左子树时做 RR 调整
4. 连接好调整后的子树，它可能作为整棵树的根，或作为 a 原来的父节点的相应方向的子结点（左子结点或右子结点）

代码实现

class AVLNode(object):
    def __init__(self, value, left, right, bf):
        self.value = value
        self.left = left
        self.right = right
        self.bf = bf

def LL(a, b): # LL 型调整
    a.left = b.right
    b.right = a
    a.bf = b.bf = 0
    return b

def RR(a, b): # RR 型调整
    a.right = b.left
    b.left = a
    a.bf = b.bf = 0
    return b

def LR(a, b): # LR 型调整
    c = b.right
    a.left, b.right = c.right, c.left
    c.left, c.right = b, a
    if c.bf == 0: # c 本身就是插入结点
        a.bf= b.bf= 0
    elif c.bf == 1: # 新结点在 c 的左子树
        a.bf = -1
        b.bf = 0
    else: # 新结点在 c 的右子树
        a.bf = 0
        b.bf = 1
    c.bf = 0
    return c

def RL(a, b): # RL 型调整
    c = b.left
    a.right, b.left = c.left, c.right
    c.left, c.right = a, b
    if c.bf == 0: # c 本身就是新结点
        a.bf = 0
        b.bf = 0
    elif c.bf == 1: # 新结点在 c 的左子树
        a.bf = 0
        b.bf = -1
    else: # 新结点在 c 的右子树
        a.bf = 1
        b.bf = 0
    c.bf = 0
    return c
        
def insert(root, value):
    a = p = root
    if a is None: # 若是一棵空树
        root = AVLNode(value, None, None, 0)
        return
    pa = q = None # 维持 pa, q 为 a, p 的父节点
    while p is not None:
        if p.bf != 0:
            pa, a = q, p # 已知最小非平衡子树
        q = p
        if value < p.value:
            p = p.left
        else:
            p = p.right
    # q 是插入点的父节点, pa, a记录最小非平衡子树
    node = AVLNode(value, None, None, 0)
    if value < q.value:
        q.left = node # 作为左子结点
    else:
        q.right = node # 作为右子结点
    # 新结点已插入，a 是最小不平衡子树
    if value < a.value: # 新结点在 a 的左子树
        p = b = a.left
        d = 1
    else:
        p = b = a.right
        d = -1
    # 修改 b 到新结点路径上各结点的 bf 值, b 为 a 的子结点
    while p != node: # node 一定存在，不用判断 b 空
        if value < p.value: # p 的左子树增高
            p.bf =  1
            p = p.left
        else:
            p.bf = -1
            p = p.right
    if a.bf == 0: # a 的原 bf 为 0，不会失衡
        a.bf = d
        return
    if a.bf == -d: # 新结点在较低子树里
        a.bf = 0
        return
    # 新结点在较高子树，失衡，必须调整
    if d == 1: # 新结点在 a 的左子树
        if b.bf == 1:
            b = LL(a, b) # LL
        else:
            b = LR(a, b) # RL
    else: # 新结点在 a 的右子树
        if b.bf == -1:
            b = RR(a, b) # RR 调整
        else:
            b = RL(a, b) # RL 调整
    if pa is None: # 原 a 为树根，修改 root
        root = b
    else:
        if pa.left == a:
            pa.left = b
        else:
            pa.right = b

# 以下为加入一些遍历与输入操作后的代码
# -*- coding: utf-8 -*-
"""
Created on Sat Jan  9 19:45:52 2021

@author: Ericaaaaaaaa
"""

class AVLNode(object):
    def __init__(self, value, left, right, bf):
        self.value = value
        self.left = left
        self.right = right
        self.bf = bf
    def __str__(self):
        return "[AVLNode value: {0} bf: {1}]".format(self.value, self.bf)
    
def insert(root, value):
    a = p = root
    if a is None:
        root = AVLNode(value, None, None, 0)
        return
    pa = q = None # 维持 pa, q 为 a, p 的父节点
    while p is not None:
        if p.bf != 0:
            pa, a = q, p # 已知最小非平衡子树
        q = p
        if value < p.value:
            p = p.left
        else:
            p = p.right
    # q 是插入点的父节点, pa, a记录最小非平衡子树
    node = AVLNode(value, None, None, 0)
    if value < q.value:
        q.left = node # 作为左子结点
    else:
        q.right = node # 作为右子结点
    # 新结点已插入，a 是最小不平衡子树
    if value < a.value: # 新结点在 a 的左子树
        p = b = a.left
        d = 1
    else:
        p = b = a.right
        d = -1
    # 修改 b 到新结点路径上各结点的 bf 值, b 为 a 的子结点
    while p != node: # node 一定存在，不用判断 b 空
        if value < p.value: # p 的左子树增高
            p.bf =  1
            p = p.left
        else:
            p.bf = -1
            p = p.right
    if a.bf == 0: # a 的原 bf 为 0，不会失衡
        a.bf = d
        return
    if a.bf == -d: # 新结点在较低子树里
        a.bf = 0
        return
    # 新结点在较高子树，失衡，必须调整
    if d == 1: # 新结点在 a 的左子树
        if b.bf == 1:
            b = LL(a, b) # LL
        else:
            b = LR(a, b) # RL
    else: # 新结点在 a 的右子树
        if b.bf == -1:
            b = RR(a, b) # RR 调整
        else:
            b = RL(a, b) # RL 调整
    if pa is None: # 原 a 为树根，修改 root
        root = b
    else:
        if pa.left == a:
            pa.left = b
        else:
            pa.right = b
    
def LL(a, b):
    a.left = b.right
    b.right = a
    a.bf = b.bf = 0
    return b

def RR(a, b):
    a.right = b.left
    b.left = a
    a.bf = b.bf = 0
    return b

def LR(a, b):
    c = b.right
    a.left, b.right = c.right, c.left
    c.left, c.right = b, a
    if c.bf == 0: # c 本身就是插入结点
        a.bf= b.bf= 0
    elif c.bf == 1: # 新结点在 c 的左子树
        a.bf = -1
        b.bf = 0
    else: # 新结点在 c 的右子树
        a.bf = 0
        b.bf = 1
    c.bf = 0
    return c

def RL(a, b):
    c = b.left
    a.right, b.left = c.left, c.right
    c.left, c.right = a, b
    if c.bf == 0: # c 本身就是新结点
        a.bf = 0
        b.bf = 0
    elif c.bf == 1: # 新结点在 c 的左子树
        a.bf = 0
        b.bf = -1
    else: # 新结点在 c 的右子树
        a.bf = 1
        b.bf = 0
    c.bf = 0
    return c

def print_tree(root):
    queue = []
    now = root
    while not((len(queue) == 0) and (now == None or now.value == None or now.value == "None")):
        print(now)
        left = now.left
        right = now.right
        if not(left == None or left.value == None or left.value == "None"):
            queue.append(left)
        if not(right == None or right.value == None or right.value == "None"):
            queue.append(right)
        if(len(queue) == 0):
            now = None
        else:
            now = queue.pop(0)
        
initial = int(input())
root = AVLNode(initial, None, None, 0)
while True:
    l = input()
    if l == "finish":
        break
    else:
        insert(root, int(l))
        print_tree(root)

内部排序问题和性质

问题定义

排序算法

基于比较的排序

基本操作、性质和评价

在讨论各个算法时，总是以被排序序列的长度（即序列中元素的个数）作为问题的规模参数 n

• 任何算法的时间复杂度都不可能优于 $O(n\log{n})$
• 算法的性质
  • 稳定性：
    • 对于待排序序列里的任一对排序码相同的记录 $R_i$ 和 $R_j$，在排序后的序列里 $R_i$ 和 $R_j$ 的前后顺序不变
    • 稳定性是一个具体算法的性质，而不是排序方法的性质
  • 适应性：
    • 如果一个排序算法对接近有序的序列工作的更快，就称这种算法具有适应性

简单排序算法

插入排序

算法的思路

1. 从一个没有元素的列表开始
2. 选择一个未排序的元素
3. 将所选元素与列表中的元素一一比较，并插入到正确的位置
4. 重复 2、3 直至所有元素都被插入到列表中为止。

代码

def insert_sort(lst):
    for i in range(1, len(lst)): # 开始时片段 [lst[0]] 已排序
        x = lst[i] # 选择元素
        j = i
        while j > 0 and lst[j-1] > x: # 逐一向前比较
            lst[j] = lst[j-1] # 反序逐个后移元素，决定插入位置
            j -= 1
        lst[j] = x
    return lst # 有没有都行，因为 python 其实已经改变了原有的 lst 了

复杂度分析

• 平均时间复杂度： $O(n^2)$
• 最坏时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$

算法特性分析

• 有稳定性

  lst[j-1] > x

• 有适应性

改进

采用二分法检索插入位置

选择排序

算法思路

1. 顺序扫描未排序序列中的元素，记住遇到的最小的元素
2. 将最小元素于未排序的第一位交换
3. 重复 1、2，直至序列排序完毕

代码

def select_sort(lst):
    """选择排序"""
    for i in range(len(lst) - 1): # 只需循环 len(lst) - 1 次
        k = i
        for j in range(i, len(lst)): # k 是已知最小元素的位置
            if lst[j] < lst[k]:
                k = j
        if i != k: # lst[k] 是已知确定最小的元素，检查是否需要交换
            lst[i], lst[k] = lst[k], lst[i] # 交换
    return lst # 有没有都行，因为 python 其实已经改变了原有的 lst 了

复杂度分析

• 平均时间复杂度： $O(n^2)$
• 最坏时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$

算法特性分析

• 没有适应性

  任何情况下的时间复杂度都是 $O(n^2)$

堆排序

补充知识

优先队列

优先队列是一种缓存结构，保证在任何时候访问或弹出的，总是当时这个结构里保存的所有元素里优先级最高的（在存数数据时会同时存入优先级）

树形结构和堆

堆及其性质

• 采用树形结构实现优先队列的一种有效技术称为堆。
• 从结构上看，堆就是结点里存储数据的完全二叉树
• 堆序：任意一个结点里存储的数据的优先级先于（或等于）其子节点里的数据
  • 堆中优先级最高的元素必在堆顶
  • 大顶堆 & 小顶堆

优先队列的堆实现

插入元素和向上筛选

弹出元素和向下筛选

算法思路

代码

def heap_sort(elems): # 堆排序
    """
    堆排序：
    采用小顶堆，因此输出顺序为从大到小
    若希望得到从小到大的输入，只需要将 ① 与 ② 处改为 ">" 即可
    """
    def siftdown(elems, e, begin, end): # elems 按层序方式存储的堆，e 为要插入的元素（向下筛选），begin, end 为已有堆的 begin, end 下标
        i, j = begin, begin*2+1 # j 为 i 的左子结点
        while j < end: # invariant: j == 2 *i + 1
            if j+1 < end and elems[j+1] < elems[j]: # ① # 使得 j 为 i 子结点中最小的结点的下标
                j += 1 # elems[j] 小于等于其兄弟结点的数据
            if e < elems[j]: # e 在三者中最小 ②
                break
            elems[i] = elems[j] # elems[j] 最小，上移
            i, j = j, 2*j+1 # i 下移， j 为 i 的左子结点
        elems[i] = e # 将 e 放入合适的位置（i 处的元素已经被移走）
        
    end = len(elems)
    # 循环建堆
    for i in range(end//2, -1, -1): # 从最下层开始，逐步向上使得序列满足小顶堆条件
        siftdown(elems, elems[i], i, end)
    # 循环逐个取出最小元素，将其积累在表的最后，放一个退一步
    for i in range((end-1), 0, -1):
        e = elems[i]
        elems[i] = elems[0]
        siftdown(elems, e, 0, i)

复杂度分析

• 时间复杂度：$O(n\log{n})$
• 空间复杂度：$O(1)$

算法特性分析

交换排序（冒泡排序）

算法思路

通过交换元素消除逆序

代码

def bubble_sort(lst):
    """冒泡排序"""
    for i in range(len(lst)):
        found = False
        for j in range(1, len(lst) - i):
            if lst[j-1] > lst[j]: # 找到逆序
                lst[j-1], lst[j] = lst[j], lst[j-1]
                found =True
        if not found: # 如果序列中已经没有逆序了
            break
    return lst # 有没有都行，因为 python 其实已经改变了原有的 lst 了

复杂度分析

• 平均时间复杂度： $O(n^2)$
• 最坏时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$

算法特性分析

• 有稳定性

• 有适应性

  if not found:

快速排序

算法思路

1. 若序列长度为 0 或 1，证明已经完成排序，返回，若不然，执行 2
2. 取待排序序列中的任意一个元素（通常是第一个）作为标准
3. 将其他元素与之比较，并分成【比标准小】、【比标准大】两部分
4. 将分好的两部分视为新的未排序序列，递归执行 2 操作

代码

def qsort_rec(lst, l, r):
    if l >= r:
        return # 分段无记录或只有一个记录
    i, j = l, r
    pivot = lst[i] # lst[i] 是初始空位
    while i < j: # 找 pivot 的最终位置
        while i < j and lst[j] > pivot:
            j -= 1 # 用 j 向左扫描找小于 pivot 的记录
        if i < j:
            lst[i] = lst[j]
            i += 1 # 小记录移到左边
        while i < j and lst[i] <= pivot:
            i += 1 # 用 i 向右扫描找大于 pivot 的记录
        if i < j:
            lst[j] = lst[i]
            j -= 1 # 大记录移到右边
    lst[i] = pivot # 将 pivot 存入其最终位置
    qsort_rec(lst, l, i-1) # 递归处理左半区间
    qsort_rec(lst, i+1, r) # 递归处理右半区间

lst = [1,6,4,3,2,7,8,9,5]
qsort_rec(lst, 0, len(lst) - 1)
print(lst)

复杂度分析

• 平均时间复杂度： $O(n\log{n})$
• 最坏时间复杂度：$O(n)$
• 空间复杂度：$O(\log{n})$

算法特性分析

• 不稳定
• 不具有适应性

归并排序

算法思路

1. 开始时，将每个记录看成单独的有序序列，则 n 个待排序的记录就是 n 个长度为 1 的有序子序列
2. 对所有有序子序列进行两两归并，得到 n/2 个长度为 2 或 1 的有序子序列——一趟归并
3. 重复 2，直到得到长度为 n 的有序序列为止。

代码

def merge(lfrom, lto, low, mid, high):
    """
    归并排序最下层函数
    实现表中相邻的一对有序序列的归并工作，将归并的结果存入另一个顺序表里的相同位置
    需要归并的两有序段分别为：lfrom[low:mid] 和 lfrom[mid:high]
    归并结果应存入 lto[low:high]
    """
    i, j, k = low, mid, low # i, j 遍历两个有序子序列，k 写入结果序列
    while i < mid and j < high: # 反复赋值两分段首最小的
        if lfrom[i] <= lfrom[j]:
            lto[k] = lfrom[i]
            i += 1
        else:
            lto[k] = lfrom[j]
            j += 1
        k += 1
    while i < mid: # 复制第一段剩余记录
        lto[k] = lfrom[i]
        i += 1
        k += 1
    while j < high: # 复制第二段剩余记录
        lto[k] = lfrom[j]
        j += 1
        k += 1
        
def merge_pass(lfrom, lto, llen, slen):
    """
    归并排序中间层函数
    实现对整个表里顺序各对有序序列的归并，完成一遍归并，
    各对序列的归并结果顺序存入另一顺序表里的同位置分段
    slen: 需要归并的每小段长度
    llen: 序列总长度
    """
    i = 0
    while i + 2 * slen < llen: # 归并长 slen 的两段
        merge(lfrom, lto, i, i + slen, i + 2 * slen)
        i += 2 * slen
    if i + slen < llen: # 剩下两端，后段长度小于 slen
        merge(lfrom, lto, i, i + slen, llen)
    else: # 只剩下一段，复制给表 lto
        for j in range(i, llen):
            lto[j] = lfrom[j]
            
def merge_sort(lst):
    """
    归并排序主函数（最顶层函数）
    在两个顺序表中往复执行中间层操作，直至排序全部完成
    """
    slen, llen = 1, len(lst)
    templst = [None] * llen
    while slen < llen: # 未形成长度为总长度的顺序序列
        merge_pass(lst, templst, llen, slen)
        slen *= 2
        # 排序完成时，结果可能存放在 templst 中，无论如何，再执行一次下一步，将结果存回 lst 中
        merge_pass(templst, lst, llen, slen) # 结果存回原位
        slen *= 2

复杂度分析

• 时间复杂度：$O(n\log{n})$
• 空间复杂度：$O(n)$

算法特性分析

• 有稳定性
• 无适应性

其他排序方法

分配排序和基数排序

算法思路

如果关键码只有很少几个不同的值，

1. 为每个关键码设置一个桶
2. 遍历序列，根据关键码把记录放在不同的桶中
3. 顺序手机各个桶的记录，得到排序的序列

复杂度分析

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

多轮分配和排序

算法思路

• 高位优先（Most Significant Digit first, MSD）
• 低位优先（Least Significant Digit first, LSD）

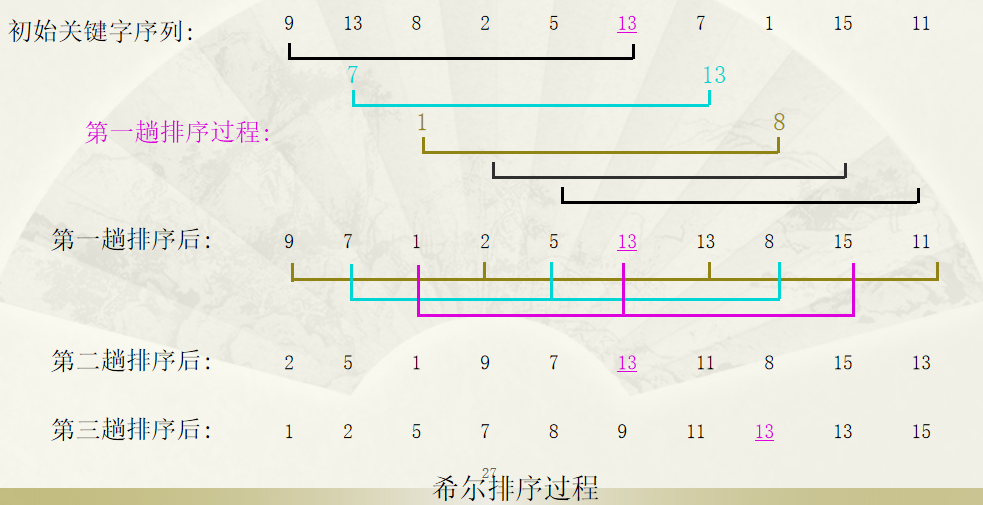
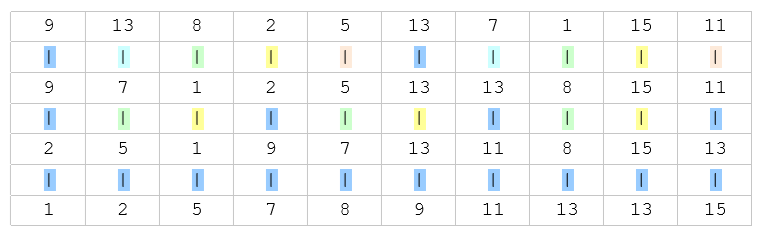
希尔排序 Shell Sort

算法思路

1. 先取一个正整数d1(d1<n)作为第一个增量，将全部n个记录分成d1组，把所有相隔d1的记录放在一组中，即对于每个k(k=1, 2, … d1)，R[k], R[d1+k], R[2d1+k] , …分在同一组中，在各组内进行直接插入排序。这样一次分组和排序过程称为一趟希尔排序；
2. 取新的增量d2<d1，重复 1 的分组和排序操作；直至所取的增量di=1为止，即所有记录放进一个组中排序为止。

外部排序

文件

文件的组织方式

顺序文件

索引文件

索引结构(称为索引文件)由索引表和数据表两部分

• 数据表：存储实际的数据记录
• 索引表：存储记录的关键字和记录(存储)地址之间的对照表，每个元素称为一个索引项

稠密索引

非稠密索引

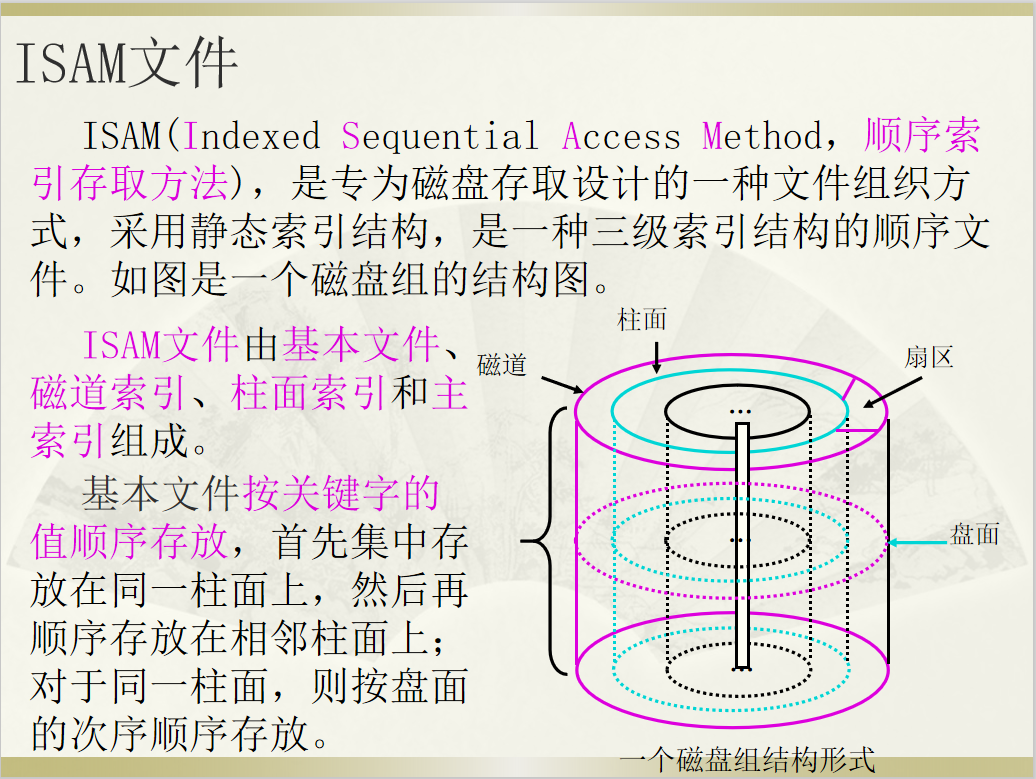
ISAM

ISAM(Indexed Sequential Access Method，顺序索引存取方法)，是专为磁盘存取设计的一种文件组织方式，采用静态索引结构，是一种三级索引结构的顺序文件。

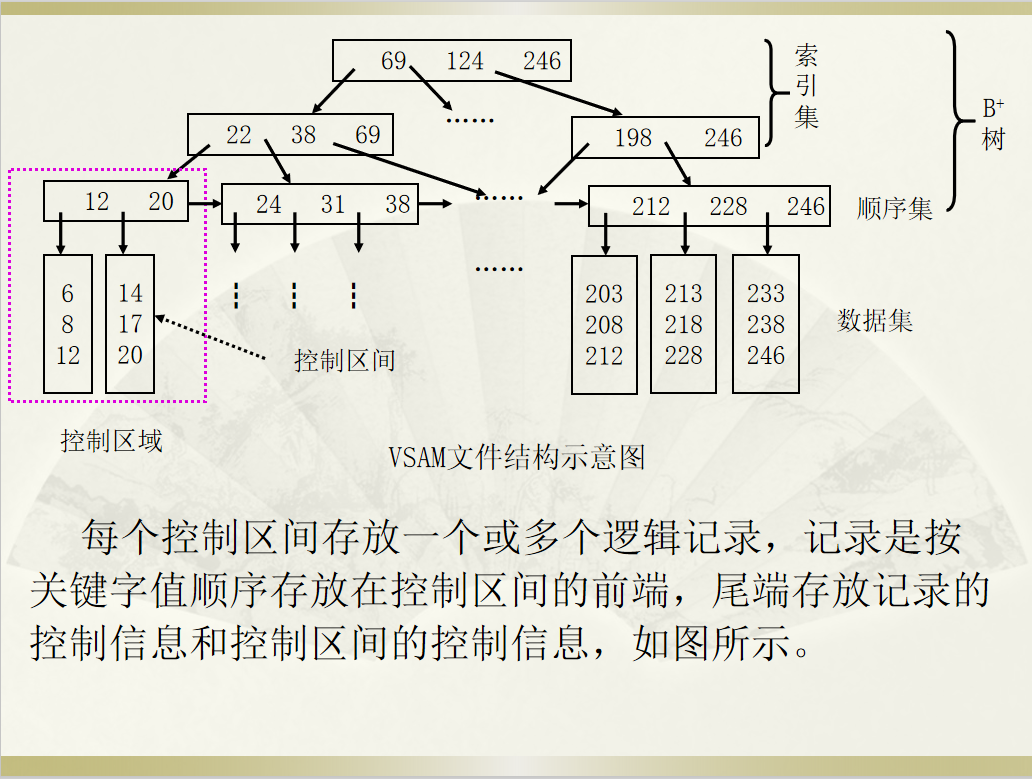
VSAM

VSAM(Virtual Storage Access Method，虚拟存取方法)，也是一种索引顺序文件组织方式，利用OS的虚拟存储器功能，采用的是基于B+树的动态索引结构。

散列文件

散列文件(直接存取文件) ：利用散列存储方式组织的文件。类似散列表，即根据文件中记录关键字的特点，设计一个散列函数和冲突处理方法，将记录散列到存储介质上。

多关键字文件

多重表文件

多重表文件(Multilist Files)的特点是：记录按主关键字的顺序构成一个串联文件(物理上的) ，并建立主关键字索引(称为主索引)；对每个次关键字都建立次关键字索引(称为次索引)，所有具有同一次关键字值的记录构成一个链表(逻辑上的)。

倒排文件

倒排文件又称逆转表文件。与多重表文件类似，可以处理多关键字查询。

外部排序

外部排序最基本的方法是归并。这种方法是由两个相对独立的阶段组成： ① 按内存(缓冲区)的大小，将n个记录的数据文件分成若干个长度为l的段或子文件，依次读入内存并选择有效的内部排序方法进行排序；然后将排好序的有序子文件重新写入到外存。子文件称为归并段或顺串。 ② 采用归并的办法对归并段进行逐趟归并，使归并段的长度逐渐增大，直到最后合并成只有一个归并段的文件—排好序的文件。

内存管理

兄弟伙伴算法

伙伴系统是一种非顺序内存管理方法，不是以顺序片段来分配内存，是把内存分为两个部分，只要有可能，这两部分就可以合并在一起; 且这两部分从来不是自由的，程序可以使用伙伴系统中的一部分或者两部分都不使用。与边界标识法类似，所不同是：无论占用块或空闲块，其大小均为2的k次幂。

当程序释放所占用的块时，系统将该新的空闲块插入到可利用空闲表中，需要考虑合并成大块问题。在伙伴系统中，只有“互为伙伴”的两个子块均空闲时才合并；即使有两个相邻且大小相同的空闲块，如果不是“互为伙伴” (从同一个大块中分裂出来的)也不合并。

设要回收的空闲块的首地址是p，其大小为2k的，算法思想是： ⑴ 判断其 “互为伙伴”的两个空闲块是否为空： 若不为空，仅将要回收的空闲块直接插入到相应的子表中；否则转⑵； ⑵ 按以下步骤进行空闲块的合并： ◆ 在相应子表中找到其伙伴并删除之； ◆ 合并两个空闲块； ⑶ 重复⑵，直到合并后的空闲块的伙伴不是空闲块为止。6