Machine Learning

Tutor: $\mathscr{Andrew Ng}$

Author of the notebook: $\mathscr{ericaaaaaaaa}$

Machine Learning

A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.

Category

• Supervised Learning
• Unsupervised Learning

Categories

Supervised & Unsupervised

Supervised Learning

"right answers" given

Unsupervised Learning

no "right answers" given

Regression & Classification

Regression Problem

Predict continuous valued output.

Classification Problem

Predict discrete valued output.

Notations

Notations

m = Number of training examples

x = input variables / features

y = output variable / features

h = hypothesis

(x, y) = one training example

(xⁱ, yⁱ) = i^th training example

The learning algorithm uses the training set to find the best hypothesis h which maps from x to y.

Problem

Linear Regression

Predict Linear regression attempts to model the relationship between two variables by fitting a linear equation to observed data. A linear regression line has an equation of the form Y = a + bX, where X is the explanatory variable and Y is the dependent variable.

Loss Function (Cost Function)

Loss Function

A loss function is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" asspcoated with the event.

An optimization problem seeks to minimize a loss function.

Part I. Linear Regression

Method

Gradient Descent

Start with some initial $\theta$, and repeatedly performs the update to minimize $J(\theta)$.

• $\alpha$: learning rate
• $\theta$: parameter(s)
• $J(\theta)$: cost function

LMS Update Rule

LMS stands for least mean squares. \(J(\theta) = \frac{1}{2}\sum_{i=1}^{n}(h_\theta(x^{(i)})-y^{(i)})^2 \\ \theta_j\gets \theta_j - \alpha \frac{\part}{\part\theta_j}J(\theta) \gets \theta_j + \alpha (y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)}\)

Classification

Batch Gradient Descent (Batch GD)

Looks at every example in the entire training set on every step.

\[\theta_j\gets \theta_j - \alpha \frac{\part}{\part\theta_j}J(\theta)\]

• Computationally Expensive
• Great for convex or relatively smooth error manifolds

Stochastic Gradient Descent (SGD) (Incremental Gradient Descent)

Repeatedly run through the training set, and each time we encounter a training example, we update the parameters according to the gradient of the error with respect to that single training example only.

• doesn’t settle at global minimum (can be solved by reducing learning rate)
• faster and less computationally expensive

The Normal Equations

Matrix Derivatives

For a function $f$: $\R^{n\times d}\rightarrow \R$ mapping from n-by-d matrices to the real numbers, we define the derivative of $f$ with respect to $A$ be: \(\triangledown_A f(A) = \begin{bmatrix} \frac{\part f}{\part A_{11}} & ... & \frac{\part f}{\part A_{1d}} \\ ... & ... & ...\\ \frac{\part f}{\part A_{n1}} & ... & \frac{\part f}{\part A_{nd}} \end{bmatrix}\)

Least squares revisited

• define the matrix X to be the n-by-d matrix that contains the training examples’ input values in its rows. \(X = \begin{bmatrix}(x^{(1)})^T\\ (x^{(2)})^T\\ ...\\ (x^{(n)})^T\end{bmatrix}\)

• define $\overrightarrow{y}$ to be the n-dimensional vector containing all the target values from the training set. \(\overrightarrow{y} = \begin{bmatrix}y^{(1)}\\ y^{(2)}\\ ...\\ y^{(n)}\end{bmatrix}\)

The loss function $J$ can be represented by \(J(\theta) = \frac{1}{2}(X_\theta-\overrightarrow{y})^T(X_\theta-\overrightarrow{y})\) To minimize $J$, we set its derivatives to zero, and obtain the normal equations: \(X^TX\theta = X^T\overrightarrow{y}\) Minimize $J(\theta)$ by explicitly taking its derivatives with respect to the $\theta_j$’s, and setting them to zero. \(\theta = (X^TX)^{-1}X^T\overrightarrow{y}^3\)

Probabilistic Interpretation

Give a set of probabilistic assumptions

Under he previous probabilistic assumptions on the data. least-squares regression corresponds to finding the maximum likelihood estimate of $\theta$.

Assume that the target variables and the inputs are related via the equation $y^{(i)}=\theta^Tx^{(i)}+\varepsilon^{(i)}$.

$\varepsilon^{(i)}$ is an error term that captures either unmodeled effects or random noise. Assume that $\varepsilon^{(i)}$ are distributed according to the Gaussian distribution with mean zero and some variance $\sigma^2$, namely $\varepsilon^{(i)}\sim N(0, \sigma^2)$

$p(\varepsilon^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(\varepsilon^{(i)})^2}{2\sigma^2})$

The principle of maximum likelihood says that we should choose $\theta$ to maximize $L(\theta)$.

Instead of maximizing $l(\theta)$, we can also maximize any strictly increasing function of $L(\theta)$. In particular, the derivations will be simpler if we instead maximize the log likelihood $\mathscr{l}(\theta) = \log L(\theta) = n\log \frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{\sigma^2}\cdot\frac{1}{2}\sum_{i=1}^{n}(y^{(i)}-\theta^Tx^{(i)})^2$.

Locally Weighted Linear Regression (LWR)

Is a kind of non-parametric algorithm.

non-parametric algorithm

Algorithms that do not make strong assimptions about the form of the mapping function. By not making assumptions, they are free to learn any functional form from the training data.

Pros

• Flexibility: capable of fitting a large number of functional forms
• Power: No assumptions (or weak assumptions) about the underlying function
• Performance: Can result in higher performance models for prediction

Cons

• More data: require a lot more training data to estimate the mapping function
• Slower: A lot slower to train as they often have a far more parameters to train
• Overfitting: More of a risk to overfit the training data and it is harder to explain why specific predictions are made.

parametric algorithm

AS learning model that summarizes the data with a set of parameters of fixed size.

1. Select a form for the function.
2. Learn the coefficients for the function from the training data.

underfitting

The model cannot capture the underlying trend of the data

• cause
  • too few data
  • the learning model is too easy and flexible
• solution
  • Increase model complexity.
  • Increase the number of features, performing feature engineering.
  • remove noise from the data.
  • Increase the number of epochs or increase the duration of training to get better results.

overfitting

The model contains too many detail and noise

• cause
  • non-parametric and non-linear methods
• solution
  • Increase training data
  • Reduce model complexity
  • Early stopping during the training phase
  • Ridge Regularization and Lasso Regularization
  • Use dropout for neural networks to tackle overfitting

Procedure of LWR

1. Fit $\theta$ to minimize $\sum_i\bold{w^{(i)}}(y^{(i)}-\theta^Tx^{(i)})^2$
2. Output of $\theta^Tx$

The $w^{(i)}$’s are non-negative valued weights.

A fairly standard choice for the weight is $w^{(i)}=\exp{(-\frac{(x^{(i)}-x)^2}{2\tau^2})}$

• $\tau$: The bandwidth parameter

Part II. Classification and Logistic Regression

Logistic Regression

Logistic Function (Sigmoid Function)

\[g(z) = \frac{1}{1+e^{-z}}\]

Squeeze the input into range [0, 1)

Digression: The perceptron learning algorithm

\[g(z)\left\{\begin{array}{l} 1 & if\ z\ge 0\\ 0 & if\ z < 0\end{array}\right.\\ h_\theta(x)=g(\theta^T x)\in\{0,1\}\\ \theta_j\gets \theta_j + \alpha(y^{(i)}-h_\theta(x)^{(i)})x_j^{(i)}\]

• $\alpha$: learning rate

Usage: 0-1 Classification Problem

Another Algorithm for Maximizing $\mathscr{l}(\theta)$

Using Newton’s method to find the maximum of $\mathscr{l}(\theta)$.

Part III. Generalized Linear Models

The Exponential Family

A class of distributions is in the exponential family if it can be written in the form: (probability distribution function) \(p(y;\eta)=b(y)\frac{\exp{(\eta^TT(y))}}{\exp({\alpha(\eta)})}\)

• $y$: data
• $b(y)$: base measure
• $\eta$: natural parameter (canonical parameter)
• $T(y)$: sufficient statistic (in this example, T(y) == y)
• $\alpha(\eta)$: log partition function
• $e^{-\alpha(\eta)}$: normalization constant

The Bernoulli Distributions

Bernoulli Distributions: a distribution over $y\in{0,1}$

\[\left\{ \begin{array}{l} p(y=1;\phi) = \phi\\ p(y=0;\phi) = 1-\phi \end{array} \right.\\ p(y;\phi) = \exp((\log(\frac{\phi}{1-\phi}))y+\log(1-\phi))\]

where \(\eta = \log{(\frac{\phi}{1-\phi})} \\ T(y)=y\\ \alpha(\eta)=-\log(1-\phi)=\log(1+e^\eta)\\ b(y)=1\)

The Gaussian Distributions

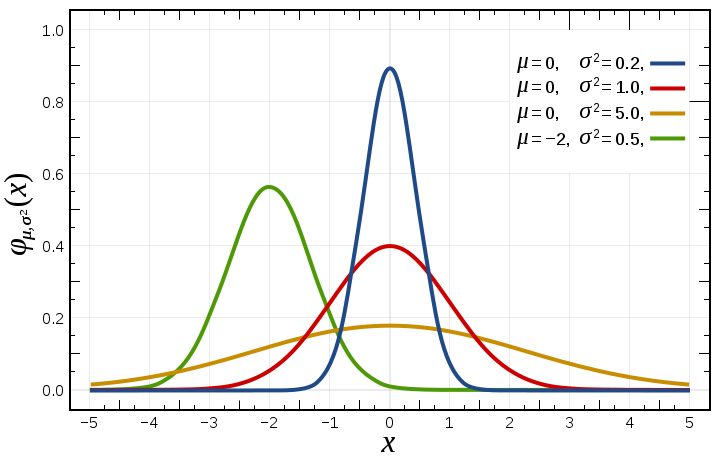\(p(y;u)=\frac{1}{\sqrt{2\pi}}\exp{(-\frac{1}{2}y^2)}\cdot\exp(\mu y-\frac{1}{2}\mu^2)\) where \(\eta = \mu\\ T(y) = y\\ \alpha(\eta) = \mu^2/2 = \eta^2/2\\ b(y) = (1/\sqrt{2\pi})\exp{(-y^2/2)}\)

Constructing GLMs (Generalized Linear Model)

Assumptions

1. $y	x;\theta\sim$ ExponentialFamily($\eta$). I.e., given $x$ and $\theta$, the distribution of $y$ follows some exponential family distribution, with parameter $\eta$.

2. Given $x$, our goal is to predict the expected value of $T(y)$.
3. The natural parameter $\eta$ and the inputs $x$ are related linearly: $\eta=\theta^T x$.

Ordinary Least Squares

• The target variable $y$ (also called response variable in GLM terminology) is continuous
• The conditional distribution of $y$ given $x$ as a Gaussian $N(\mu,\sigma^2)$

$h_\theta(x)=E[y

x;\theta]=\mu=\eta=\theta^Tx$

Logistic Regression

• Binary classification, $y\in{0,1}$
• Bernoulli distrubution

$h_\theta(x)=E[y

x;\theta]=\phi=1/(1+e^{-\eta})=1/(1+e^{-\theta^Tx})$

Canonical Response Function: the function $g$ giving the distribution’s mean as a function of the natural parameter

Canonical Link Function: the inverse of $g$, namely $g^{-1}$

Softmax Regression

• $y\in{1,2,…,k}$

\[p(y;\phi)=b(y)\exp{(\eta^T(y)-\alpha(\eta))}\]

where \(T(1)= \left[ \begin{array}{c} 1\\0\\0\\...\\0 \end{array} \right]\quad T(2)= \left[ \begin{array}{c} 0\\1\\0\\...\\0 \end{array} \right]\quad ...\quad T(k-1)= \left[ \begin{array}{c} 0\\0\\0\\...\\1 \end{array} \right]\quad T(k)= \left[ \begin{array}{c} 0\\0\\0\\...\\0 \end{array} \right] \\ \eta= \left[ \begin{array}{c} \log{(\phi_1/\phi_k)}\\ \log{(\phi_2/\phi_k)}\\ ...\\ \log{(\phi_{k-1}/\phi_k)} \end{array} \right]\\ \alpha(\eta) = -\log{(\phi_k)}\\ b(y)=1\) The log-likelihood \(\mathscr{l}(\theta) = \sum_{i=1}^{n}\log\prod_{l=1}^k(\frac{e^{\theta_l^Tx^{(i)}}}{\sum_{j=1}^{k}e^{\theta_j^Tx^{(i)}}})^{1\{y^{(i)}=l\}}\)

Part IV. Generative Learning Algorithms

Discriminative Algorithm: Learn mapping directly from the space of inputs $\chi$ to the labels ${0, 1}$. (learn $p(y

x)$)

Generative Algorithm: Distinguish different classes by training different model for different classes. (learn $p(x

y)$ and $p(y)$)

The $p(y)$ can be called as class priors.

\[p(y|x)=\frac{p(x|y)p(y)}{p(x)}\]

Gaussian Discriminant Analysis (GDA)

GDA – Gaussian Discriminant Analysis

Suppose $x\in\R^n$

Assume that $p(x

y)$ is distributed according to a multivariate normal distribution.

The multivariate Normal Distribution

The multivariate normal distribution in $d$-dimensions, also called the multivariate Gaussian distribution, is parameterized by a mean vector $\mu\in\R^d$ and a covariance matrix $\sum\in\R^{d\times d}$, where $\sum\ge 0$ is symmetric and positive semi-definite. \(p(x;\mu,\Sigma)=\frac{1}{(2\pi)^{d/2}|\Sigma|^{1/2}}\exp{(-\frac{1}{2}(x-\mu )^T\Sigma^{-1}(x-\mu))}\)

$

\Sigma

$ denotes the determinant of matrix $\Sigma$.

A Gaussian with zero mean and identity covariance is also called the standard normal distribution.

The Gaussian Discriminant Analysis Model

A classification problem in which the input features $x$ are continuous-valued random variables, we can then use the Gaussian Discriminant Analysis (GDA) model, which models $p(x

y)$ using a multivariate normal distribution.

The model is: \(y\sim Bernoulli(\phi)\\ x|y=0\sim N(\mu_0,\Sigma)\\ x|y=1\sim N(\mu_1, \Sigma)\) the distribution: \(p(y)=\phi^y(1-\phi)^{1-y}\\ p(x|y=0)=\frac{1}{(2\pi)^{d/2}|\Sigma|^{1/2}}\exp{(-\frac{1}{2}(x-\mu_0 )^T\Sigma^{-1}(x-\mu_0))}\\ p(x|y=1)=\frac{1}{(2\pi)^{d/2}|\Sigma|^{1/2}}\exp{(-\frac{1}{2}(x-\mu_1 )^T\Sigma^{-1}(x-\mu_1))}\) The parameters of our model are $\phi$, $\Sigma$, $\mu_0$, and $\mu_1$.

The likelihood of the data is given by: \(l(\phi, \mu_0, \mu_1, \Sigma)=\log{\prod^n_{i=1}p(x^{(i)}|y^{(i)};\mu_0,\mu_1,\Sigma)p(y^{(i)};\phi)}\) By maximizing $l$ with respect to the parameters, we find the maximum likelihood estimate of the parameters to be: \(\phi=\frac{1}{n}\sum_{i=1}^{n}1\{y^{(i)}=1\}\\ \mu_0=\frac{\sum_{i=1}^n 1\{y^{(i)}=0\}x^{(i)}}{\sum_{i=1}^n 1\{y^{(i)}=0\}}\\ \mu_1=\frac{\sum_{i=1}^n 1\{y^{(i)}=1\}x^{(i)}}{\sum_{i=1}^n 1\{y^{(i)}=1\}}\\ \Sigma=\frac{1}{n}\sum_{i=1}^n(x^{(i)}-\mu_{y^{(i)}})(x^{(i)}-\mu_{y^{(i)}})^T\)

Discussion: GDA and logistic regression

GDA makes stronger modeling assumptions about the data than does logistic regression.

Specifically, when $p(x

y)$ is indeed gaussian (with shared $\Sigma$), then GDA is asymptotically efficient.

Logistic regression is more robust and less sensitive to incorrect modeling assumptions.

Summarization:

• GDA makes stronger modeling assumptions, and is more data efficient (i.e. requires less training data to learn “well”) when the modeling assumptions are correct or at least approximately correct.
• Logistic regression makes weaker assumptions, and is significantly more robust to deviations from modeling assumptions.

Naive Bayes

The problem in which $x_j$’s are discrete-valued.

Naive Bayes (NB) assumption: assume that the $x_i$’s are conditionally independent given $y$. The resulting algorithm is called Naive Bayes classifier. \(p(x_1,...,x_d|y)=\prod_{j=1}^d p(x_j|y)\) Given a training set ${(x^{(i)},y^{(i)});i=1,…,n}$, the joint likelihood of the data is: \(L(\phi_y,\phi_{j|y=0},\phi_{j|y=1})=\prod_{i=1}^{n}p(x^{(i)},y^{(i)})\) The maximum likelihood estimates: \(\phi_{j|y=0}=\frac{\sum_{i=1}^n 1\{x_j^{(i)}=1\wedge y^{(i)}=0\}}{\sum_{i=1}^n 1\{y^{(i)}=0\}}\\ \phi_{j|y=1}=\frac{\sum_{i=1}^n 1\{x_j^{(i)}=1\wedge y^{(i)}=1\}}{\sum_{i=1}^n 1\{y^{(i)}=1\}}\\ \phi_y=\frac{\sum_{i=1}^n 1\{y^{(i)}=1\}}{n}\)

Laplace Smoothing

It is statistically a bad idea to estimate the probability of some event to zero just because you haven’t seen it before in your finite training set. Laplace smoothing (also called additive smoothing) is a technique used to smooth categorical data.

Defining the problem:

• mission: estimating the mean of multinomial random variable $z$ taking values in ${1,…,k}$
• parameterize the multinomial with $\phi_j=p(z=j)$

No laplace smoothing: \(\phi_j = \frac{\sum_{i=1}^n 1\{z^{(i)}=j\}}{n}\) With laplace smoothing: \(\phi_j = \frac{1+\sum_{i=1}^n 1\{z^{(i)}=j\}}{k+n}\)

Event Models for Text Classification

A different model, called the Multinomial event model.

Part V. Kernel Moethods

Feature Maps

• The input attributes of a problem: the “original” input value, e.g. $x$

• The featured variables, e.g. $x^0$, $x^1$, …

• The featured maps $\phi(x)$ \(\phi(x) = \left[ \begin{array}{l} 1 \\ x \\ ... \\ x^n \end{array} \right]\in \R^n\)

LMS (least mean squares) with features

Batch gradient descent update rule: \(\theta \gets \theta + \alpha\sum_{i=1}^n (y^{(i)}-\theta^T\phi(x^{(i)}))\phi(x^{(i)})\) Stochastic gradient descent update rule: \(\theta \gets \theta + \alpha (y^{(i)}-\theta^T\phi(x^{(i)}))\phi(x^{(i)})\)

where:

• $\phi: \R^d\rightarrow \R^p$: a feature map that maps attributes $x$ (in $\R^d$) to the features $\phi(x)$ in $\R^p$.
• $\theta$: a vector in $\R^p$
• $\alpha$: learning rate
• goal: fit to the function $\theta^T\phi(x)$

LMS with the kernel trick

The gradient descent update, whether it is batch or stochastic becomes computationally expensive when the features $\phi(x)$ is high-dimensional.